
今回は亀的速度の問題解説編。
問題

解説
(1)前回は$l_1$と$l_2$を求めていて、それぞれ
$l_1: y=2ax−a+1$
$l_2: y=-\dfrac{1}{2a} x -\dfrac{1}{16a^3}+1$
だった。今回は、それらを用いて(b)と(c)を考えていこう。
(b)まずはこの$C_1$がどんな場所なのか視覚的に確認してみる。
なんでそんなことするのかって、当たり前な人には超当たり前なことだけど、でも解けない人はなにも書かずに考え込んでしまうわけで、解くためにわりに重要な最初の岐路だったりする。そして、そんな当たり前な人の中にだって、なんで図を描いてみるのかと正面から問われると、解けるための習慣でこれといえるような回答をもっていない人も一定いるんじゃないだろうか(別にいいけど)。
この問題は我々に面積を問うているわけだけど、そもそも面積というのは単純な定義を参照すると、指定された領域に一辺1の正方形がいくつ入るかというものだ。それを要領よく数える術として、様々な公式が存在していると解釈できる。
とはいえ、どんなに面積を求める公式に種類があっても、莫大なパターンの形を網羅できているわけではない。それゆえに、それら公式を用いることができるように眼前の形を分解、或いは統合することを考えることになる。要は知っている形を使ってパズルを考えるようなことだ。
そういう認識があれば、いきなり数式というよりどういうピースで構成されているかを確認するために図を描くことは肝要だということがわかる。パズルを数式のみで配置決定できる人がいたとしたら、そもそもこのレベルで躓くような人物じゃない。
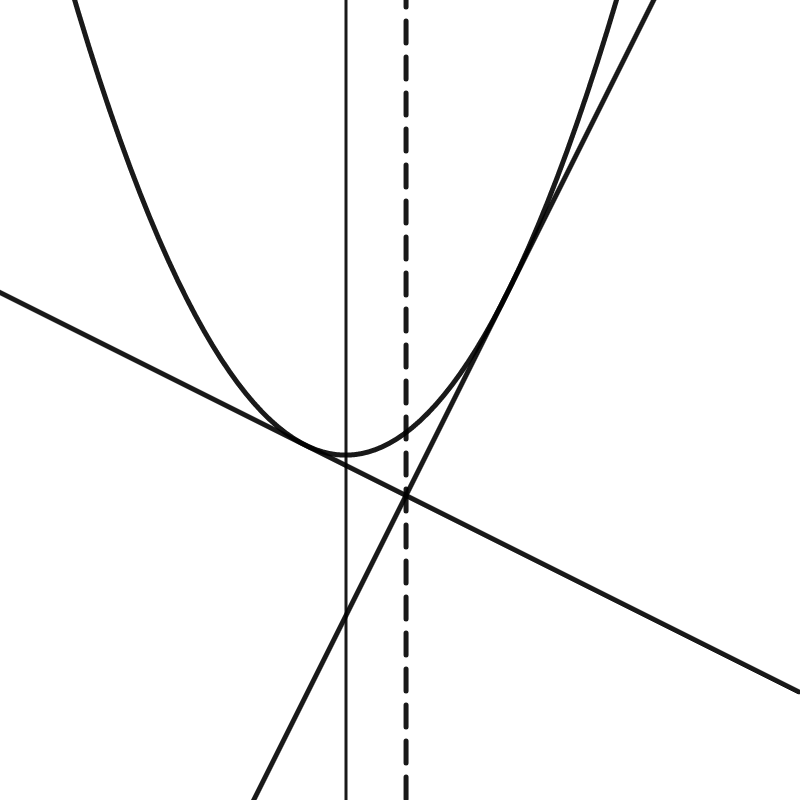
ということで、図を描くとこんな感じだ。
散々パズルの話をしておいてあれだけど、二次関数の面積を考えるためのツールは接点の$x$座標を用いた公式と、そこから発展した比のテクニックが多い。つまり裏を返せば、接線の交点の$x$座標(この問題の場合、$t$)を用いるものはあまりメジャーじゃない(多分)。
円以外で丸みを帯びた部分を含む面積は積分を考えるのが常套手段だから、ここは素直に積分で面積を求めることを考えよう。
$$ S_1 = \int_{t}^{1} (ax^2+1) - (2ax−a+1) dx $$
$$ = \int_{t}^{1} (ax^2-2ax+a) dx $$
$$ = a\int_{t}^{1} (x-1)^2 dx $$
ここで注意したいのは、この因数分解はたまたまなんかじゃないということだ。二次関数と接点が1とわかっている直線の引き算だから、当然こう表現されるし、ここから立式することもありだ。
$$ = a \left[ \dfrac{(x-1)^3}{3} \right]_{t}^{1}$$
$$\therefore \dfrac{S_1}{a}= \dfrac{(1-t)^3}{3} $$
(c)続いて、$a^2$を$t$を用いて表現する問題。そもそも$t$ってなんだったっけと振り返ると、2直線の交点なわけだから、連立して得られる解の$x$に等しい。
ここでまじめに計算してもいいんだけど、すべての二次関数は相似だということ思い出そう。思い出すというか、二次関数をみたら頭の片隅にいつもある感じだ。
ここでは、$y=x^2$とその任意の二つの接線(接点の$x$座標はそれぞれ$p$、$q$)
$$y=2px-p^2$$
$$y=2qx-q^2$$
を考えると、容易に$x$を求めることができて、
$$x=\dfrac{p+q}{2}$$
となる。すべての二次関数は相似なわけだから、この位置関係は常に成立し、交点の$x$座標は平均値であることがわかる。
ゆえにこの問題にもこれを当てはめると、
$$t=\dfrac{ -\frac{1}{4a^2} +1}{2}$$
となる。ゆえに
$$a^2=\dfrac{1}{4-8t}$$
となる。
最後に$ \dfrac{S_2}{a}$を考える。この問題、マーク式ならば、有名な面積比を用いて計算ができるけど、記述式の問題で教科書に載ってない(多分)ものをつかうのは憚られるから、まじめに計算していこう。
$l_2$と二次関数の接点を$p$とおくと、$S_1$と同様に
$$\int_{p}^{t}a(x-p)^2 dx $$
と書けるからこれを計算して、
$$=a\dfrac{(t-p)^3}{3}$$
ここで
$P= -\frac{1}{4a^2}=2t-1$
であることから
$$=a\dfrac{(1-t)^3}{3}$$
と書ける。
ゆえに
$$C_2=a\dfrac{(1-t)^3}{3}+a\dfrac{(1-t)^3}{3}=2a\dfrac{(1-t)^3}{3}$$
$$\therefore \dfrac{C_2}{a}=2\dfrac{(1-t)^3}{3}$$
となる。
今回はここまで。

