
今回やっと2019の1が終わる。このペース、毎年ながら過去問解説としてひどいけど、ポイントは材料がたまたま過去問なだけで、どうやって問題を解くかの解説なわけで、汎用性を醸し出しているところで許されていると勝手に思っている。
ということで、前回の続き。
問題

解説
今回は、面積$S(t)$の最大値を求める問題。
一般的に、関数の最大値(最小値)を求めよと問われたならば、
グラフを描いててっぺんをみる
ことを考える。平たく単純に考えれば、これされできれば答えは求められる。
つい腕を組んでしまうのは、
グラフが描けない
てっぺんがわからない
ことが原因だったりするわけで、その辺を定形的に求める武器として微分がある。
関数を微分することでなにがわかるの?
ということを今一度教科書的に立ち返ると、変化量の極限として、接線の傾きがわかるということだった。接線の傾きがわかると、例えば接線の傾きが正となるような範囲では、関数の値は増加していると判断することができる。関数が上り調子のときにその関数の接線の傾きは正になっているということは感覚的にもつかみやすいところだ。
で、最大値を求めるためにグラフを描くというのは、てっぺんを見定める為なわけで、逆に言うとその為の必要最低限の情報さえわかっていればいい。
つまり、
どの範囲において関数は増加傾向にあって、
どの範囲で減少傾向に有るのか
ということがわかればざっくりグラフは描くことができて、増加から減少に転じているところが一つポイントになるということがわかる。
そんなことを頭の片隅において、問題に取り掛かっていこう。
前回まで求めたものを再掲しておく。
$$S(t)=\sin t + \sin 3t$$
$$S'(t)=4\cos t ( 3 \cos ^2 t -2 )$$
特に、導関数$S'(t)$ はただ単に微分しただけではなく、$\cos t$だけで表現できていることも忘れてはいけない。変数とか関数の種類とか、少ないほうが考えやすいのは自明だ。
で。$S(t)$の最大値なんだから、$S(t)$のグラフを描いててっぺんをみれるばいいというのが冒頭の話。グラフを描くために、微分をするという誘導まで用意してくれていた。さぁ、グラフを描いてみよう。
与えられた定義域において導関数の符号の移り変わりをみることで、ざっくりグラフを描くことができるわけだけど、
「あれ、この$S'(t)$の符号の見方がわからない」
なんてことになっていないだろうか。
そんなあなたは、この問題が放つマヌーサにかかっている(マヌーサは、ドラクエの幻をみせる呪文)。きっと、三角関数のせいで符号の判別ができかねているのかもしれないが、三角関数ってなんだっけということをちゃんと抑えていれば大したことはない。
単位円において、点$(1, 0)$から反時計回りに$\theta$回転したとき、その単位円周上の点を$(\cos \theta, \sin \theta)$とする、というのが定義だ。$\cos \theta$はあくまで単位円周上の$x$座標の値なわけで、個性を奪い取ってやれば、
$$\cos \theta = x (-1 \leqq x \leqq 1)$$
といつもの$x$で表現することができる。
このスタンスで問題文を置き換えてみよう。文字変数を考えるときは、どんなときでも文字のとその変域(範囲)はセットだ。この問題に限らず、必ずセットだ。超スーパー自明なときには省略されることもあるけど、影がとても薄くなるだけで、存在していないわけではない。
今回、$$\cos t = x$$ とおきたい。変域がどう移り変わるかを考えると、
$$0 < t < \dfrac{\pi}{3} \Rightarrow \dfrac{1}{2} < \cos t < 1$$
となるから、
$$\dfrac{1}{2} < x < 1$$
となることがわかる。このとき$S'(t)$は
$$4\cos t ( 3 \cos ^2 t -2 )=4x ( 3 x^2 -2 )$$
と表現される。
これはただの3次関数だ。教科書的な作法ではちゃんと増減表を書かなければいけないところだけど、マーク式だから少し横着することにしよう。
3次関数は、3次の係数が正のときに
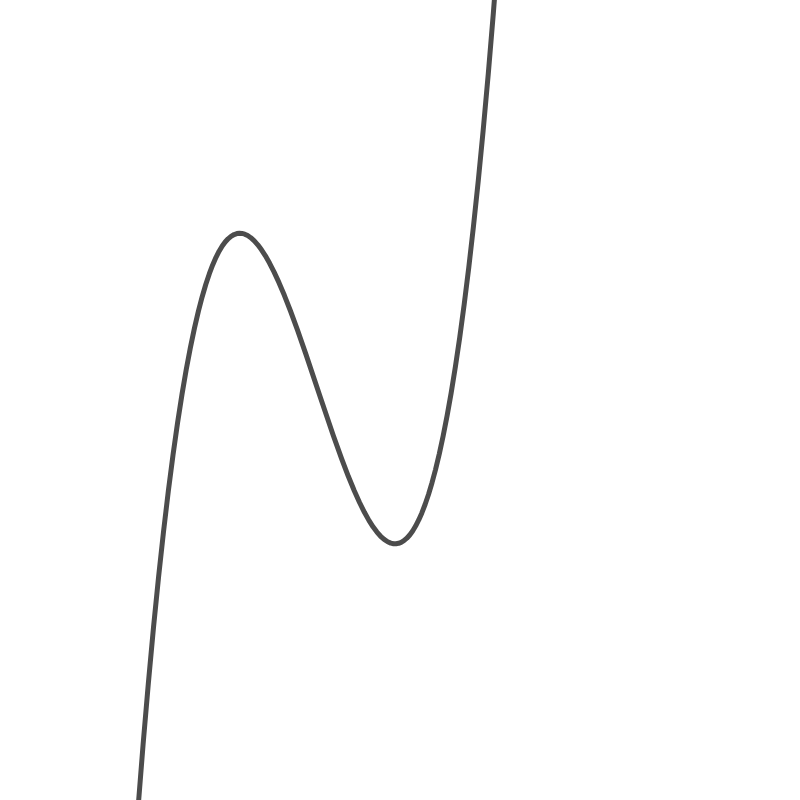
こんなグラフ(N型)になるし、逆に負のときに
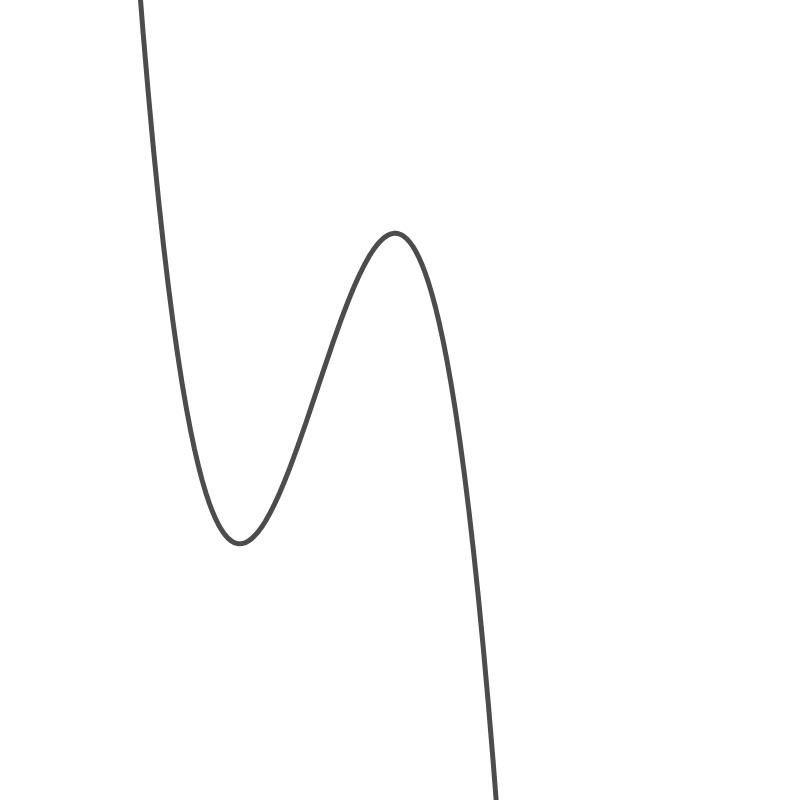
こんなグラフ(逆N型)になる。で、いま係数は正だからN型になる。
そして、傾きが正から負に変わるところで極値をもつわけで、このときの$x$の値は
$$4x ( 3 x^2 -2 )=0$$
を求めて出てくる3つの$x$のうち、一番小さいやつ$\dfrac{\sqrt{6}}{3}$とわかる。
※この辺、わからない人は丁寧に増減表を書いてみるとよろし。
で、この$x=\dfrac{\sqrt{6}}{3}$は、$\dfrac{1}{2} < x < 1$にちゃんと当てはまっている。
あとは、$S\left( \dfrac{\sqrt{6}}{3} \right)$を計算すれば終わりだ。
$S(t)$には、$\sin 3t$が含まれていて、これでは$x$で表現することができない。でも、
$3t$を$t$の表現に変えるツールこそ3倍角の公式なわけで、これを使って計算してみよう。
$$S(t)=\sin t + \sin 3t$$
$$=\sin t + 3\sin t - 4 \sin^3 t$$
$$=4\sin t - 4 \sin^3 t$$
ここで、$x=\dfrac{\sqrt{6}}{3}$だから、
$$\sin t = y = \sqrt{1-x^2}=\dfrac{\sqrt{3}}{3}$$
と表すことができて、
$$S(t)=4\dfrac{\sqrt{3}}{3} - 4\left( \dfrac{\sqrt{3}}{3} \right)^{3}= \dfrac{8\sqrt{3}}{9} $$
と求めることができた。
んー。誘導が過剰だったなぁ。以上。また次回。

