【問題解説】センター試験平成30年度本試験ⅡＢ 第２問

 最近睡眠時間のコントロールに悩み中。

5時間くらいで完全回復できるような睡眠法ってないものだろうか。とりあえず、BOSEのこれ買ってみようかな。意味あるかな。

BOSE NOISE-MASKING SLEEPBUDS ノイズマスキングイヤープラグ

今回から第2問。

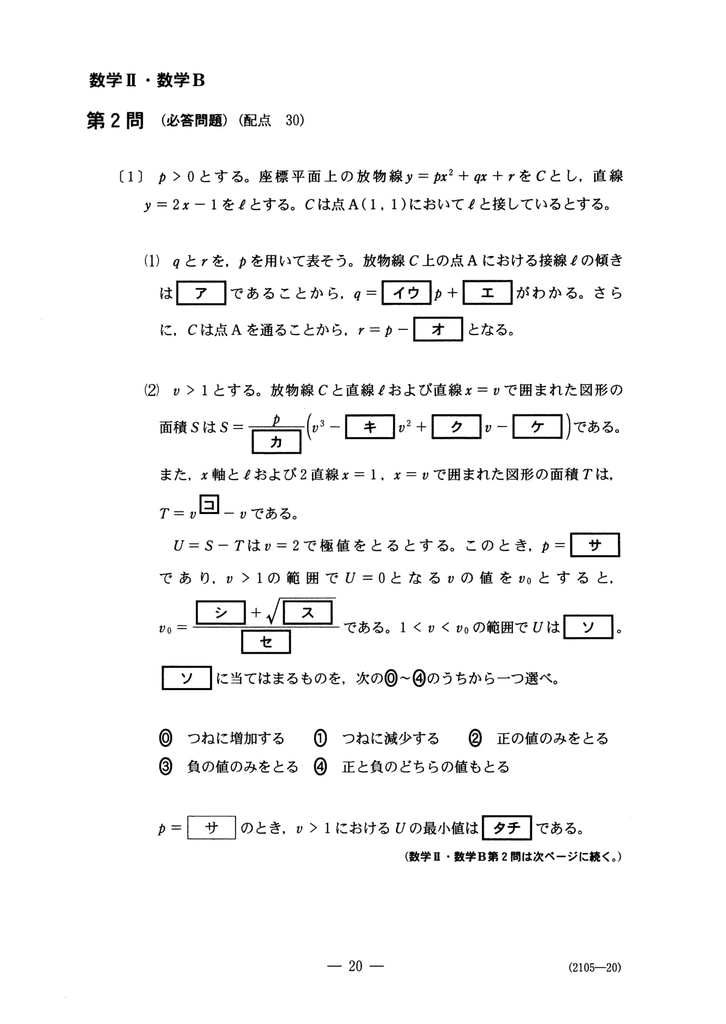
（１）

一般に、放物線はご存知の通り

$y=px^{2}+qx+r$

と表される。

各項の係数部分に未知数が３つあって（$p$、$q$、$r$）、放物線に関する情報が得られるたびそれを定量化することで未知数の姿が明らかになっていく（定量化とは数式に翻訳するということ）。

この問題では２つ条件が与えられていることから、未知数一つで表現ができるよね、だから$q$と$r$と$p$で表してねと言っている。そしてそのヒントとして、接線の傾きがあるよと教えてくれている。

じゃその２つの条件って何だっけというところから考えていこう。今考えている放物線は$C$だから、Cの出てくる文を注意深く読めば、

• $A$ を通るということ
• $A$ での接線の傾きが２であること

がみつかる。それぞれを定量化して考えてみる。

問題の中での登場順は上の箇条書きの順だけど、誘導の中では接線の傾きからのアプローチが先だから、それに倣って解いていくことにする。

接線の傾きは、導関数（微分した関数）に接点の$x$座標を代入したものだから、そのとおりの計算をすると求まるわけだが、そもそも問題の中で接線は$l$だよと教えてくれているので、計算結果は２になるとわかっている（つまりアは２）。それを実際に数式で書けば、定量化されたという状態になる。

ここで、今後の利便性の為に放物線と接線の関数をそれぞれ$f$、$g$とおく。つまり、

$f(x)=px^{2}+qx+r$

$g(x)=2x-1$

とおく。

ここで、放物線の導関数$f'$は

 $f'(x)=2px+q$

で、点$A$での接線の傾きは、

 $f'(1)=2p+q$

となる。そして、この値が２と同じだよということだ。つまり

$2p+q=2$

となる。ゆえに

$q=-2p+2$

と書けて、イウ、エが求まった。

次の条件は、$C$は$A$を通ることだった。通るってことは、$A$は放物線上の点ということなわけで、 放物線上の点なら代入したときに関数の等式を満たすということになる。

$f(1)=1=p\cdot 1+ q \cdot 1 +r$

$q$は先ほど$q=-2p+2$と書けることがわかっているので、

$p\cdot 1+ (-2p+2) \cdot 1 +r$

$\Leftrightarrow p-2p+2 +r=1$

$\Leftrightarrow r=p-1$

よって、オは1となる。

（２）

（１）は準備運動なので、ある意味でここからが本番。といっても大して難しいわけじゃないけど。まずはわかっていることを図示してみよう。

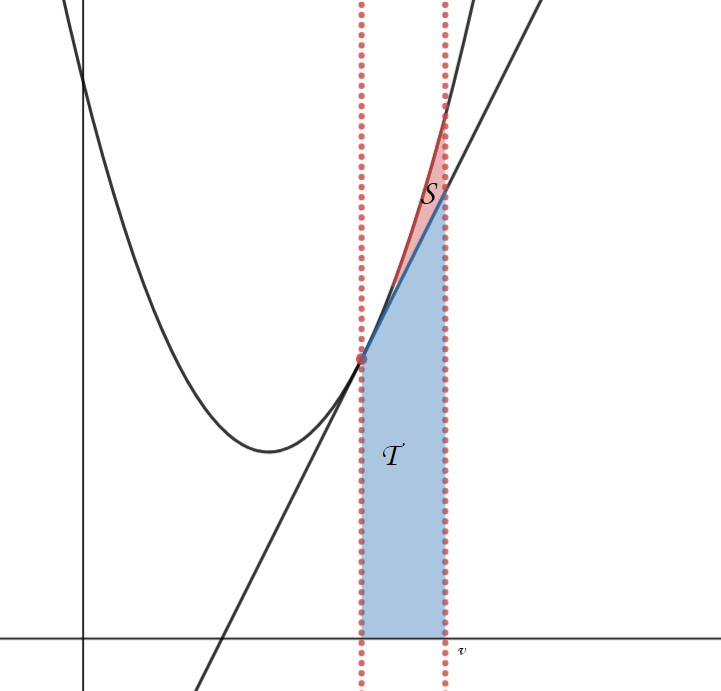
こんな感じだ（Aとか1のところとか文字おいてなくてゴメンナサイ）。

まずは$S$から計算してく。放物線と直線に囲まれた部分の面積なんて通常の幾何では解けないわけで、ここではニュートンやライプニッツに感謝しながら積分計算を行う。

$\int (f - g) dx$を計算することで該当箇所の面積を求められる（なんで？と思う人は教科書を読み直そう。いずれこのサイトでも解説したいと考えている）。

$$S=\int_{1}^{v} \left\{ f(x)-g(x) \right\} dx = \int_{1}^{v} \left\{\left(px^{2} +(-2p+2)x +p-1\right)-\left( 2x-1 \right) \right\} dx $$

 $=\left[ \dfrac{p}{3}x^{3} +\dfrac{1}{2}(-2p+2)x^{2} +(p-1)x -\left( x^{2} -x \right)  \right]_{1}^{v}$

 $=\left[ \dfrac{p}{3}x^{3} -px^{2} +px  \right]_{1}^{v}$

$=\dfrac{p}{3}v^{3} -pv^{2} +pv-\left(\dfrac{p}{3} -p +p\right)$

$=\dfrac{p}{3}\left( v^{3}-3v^{2}+3v-1  \right)$

とカ、キ、ク、ケが求まる（最後は解答欄の形に合わせて$\dfrac{p}{3}$で括りだした形に）。

次に$T$を考えよう。$T$は$x$軸と$l$と２直線$x=1$、$x=v$に囲まれた面積で、つまりは直線に囲まれた面積だ。一度積分を使った脳になるとそれに固執してしまって、面積はなんでも積分で求めるモードになる人がいるが、直線で囲まれた面積は初頭幾何で素直に考えたほうが早いことが多い。この問題の場合、$T$は台形なので、台形公式を使って解くのが手っ取り早い。

台形の面積公式

面積＝(上底＋下底)✕高さ✕$\dfrac{1}{2}$

大学受験数学を解いているときに敢えて強調するものでもないが、ここは念の為。勿論台形とは向かい合う一組の辺が平行である図形（四角形）のことで、その並行部分の長さを上底や下底と呼ぶ。 

で$T$を考えると、２直線$x=1$、$x=v$が平行な台形なわけで、それに対して公式を適用すると

$T=\left\{  1+\left( 2v-1 \right)  \right\} \cdot \left( v-1 \right) \cdot \dfrac{1}{2}$

$=v^{2}-v$

とコが求まる。ちなみにこの問題、答の形が情報持ちすぎてるから、上の計算を律儀にしなくても２次式とわかった時点で実は２と求まる。

最後に面積の差$U$を考える。$v=2$で極値をとるらしい。ということは微分して2を代入すると0になるということだ（極値が求まる逆プロセス）。

ここでも利便性のためにUを関数$h$でおくことにする。つまり

$h(x)=\dfrac{p}{3}\left( v^{3}-3v^{2}+3v-1  \right)-\left( v^{2}-v \right) $

とおく($p$を求める未来があるから、ここで無駄に展開をせぬよう)。

これを微分して2を代入すればいいわけだから、そのとおり実践すると

$h'(x)=\dfrac{p}{3}\left( 3v^{2}-6v+3 \right)-\left( 2v-1 \right)$

$h'(2)=\dfrac{p}{3}\left( 3 \cdot 2^{2}-6\cdot 2+3 \right)-\left( 2\cdot 2-1 \right)=0$

$\therefore p=3$ 

 でサが求まった。

次に$U=0$となるときを考える。これはつまり$S$と$T$が等しいときだが、定性的に考えてもいいことがなさそうなので、素直に数式で計算してみる。

$\dfrac{3}{3}\left( v^{3}-3v^{2}+3v-1  \right)-\left( v^{2}-v \right) =0$

$\Leftrightarrow v^{3}-4v^{2}+4v-1=0$

これを因数分解するのかよと思うかもしれないが、$v=1$が成り立つのは明らかなので（あ、ここで定性的に考えることに意味があったか）

$\Leftrightarrow \left(v-1\right)\left( v^{2} -3v +1 \right)=0$

とわかる。あとは解の形から右のカッコの中の式に解の公式を使うだけかとわかる。

$\dfrac{-(-3)\pm \sqrt{(-3)^{2}-4}}{2}=\dfrac{-(-3)\pm \sqrt{5}}{2}$

ここで$v>1$なので

$v_0=\dfrac{-(-3) + \sqrt{5}}{2}$

 となる（シ、ス、セ）。

次は$1<v<v_0$の範囲で$U$がどうなっているかを選択肢の中から考える問題だ。

普通だったら$h(x)$の増減表を書いて、この範囲でこの関数がどう振る舞うかを考察するんだけど（記述式ではそれを実践するところだけど）、三次関数なんて形はすでにわかっている。

最高次の係数が正だったらN字型だし、負だったら逆N字型だ。 そのことを前提に今までの情報をプロットすると

このようになる。このことから、$1<v<v_0$の範囲では負の値のみをとることからソは③であることは明らかだ。

そして$v>1$における最小値も$v=2$のときで

$h(2)=8-168-1=-1$

とわかる（タチ）。

いちいち増減表書いてたら時間がもったいないよね。

ということで、今回はここまで。

センター試験過去問研究　数学?・Ａ／?・Ｂ (2019年版センター赤本シリーズ)