【問題解説】センター試験平成30年度本試験ⅡＢ 第４問－２

金曜、月曜と更新を飛ばしてしまった。

年末が近づくと何かと忙しくなり始めるもので・・・

という言い訳をしたところで前回の続き。

問題

 解説

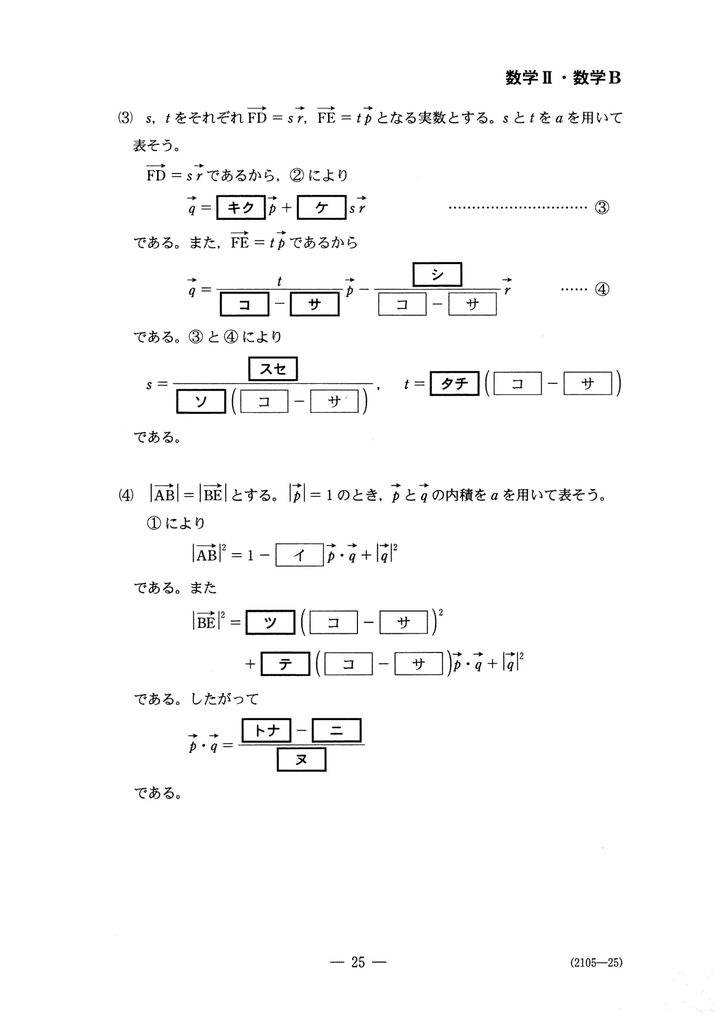
（３）この問題のゴールは$s$と$t$を$a$を用いて表すことだ。短くない問題文のときは目先の問題に目を奪われて、本流を見失ってしまうことがある。そしてそのことが重要なヒントを見落とすことにもつながるので、何をしたい問題なのかということはしっかり抑えておきたい。

ということで、③から考えていく。

$\overrightarrow{FD}=s\vec{r}$であるから

なんて因果関係のヒントがあるし、

②により

なんてこの道具を使えというメッセージもある問題だ。この両方が等式だし、求めるものも等式なので、それらをすべてつないで見れば自ずと答がでてくる易しい問題だ。

②は

$\overrightarrow{FD}=\dfrac{3}{4}\vec{p}+\dfrac{1}{4}\vec{q}$

というものだった（導出は前回参照）。

ゆえに$\overrightarrow{FD}$は、

$s\vec{r}$

とも書けるし

$\dfrac{3}{4}\vec{p}+\dfrac{1}{4}\vec{q}$

とも書けるということがわかる。

 言われれば簡単な話だけど、一般的に考えるとこれって実は奥が深い。

「＝（イコール）」ってなんですか？と問われたならば、多くの人が同じという意味だと答える。間違いじゃないけど、ほんとに同じものだったらわざわざボクらはこんな記号を用いて相手に伝えない。異なるように見えるものが実は同じだから、「＝」を使って同じだよと言うわけだ。

このことはなにも数学の世界に閉じた話ではない。

「あいつの話はいつも同じだよ」

というときは、あいつが今回話した時間や場所は前回と異なるけど（もしかすると話の内容も細部は違うけど）、概要をまとめれば同じ（「＝」）だよってことだし、

「ボクと君は一心同体だね」

なんていうときは、明らかにボクと君は存在として異なっているわけだ。

すなわち換言すると、異なるものをとある観点でつなぐ記号が「＝」と解釈できる。

数学の世界では、異なる表現だけど同じものを意味してるよってときに使いがちで、今回のケースもそれにあてはまる。

つまり、

$s\vec{r}=\dfrac{3}{4}\vec{p}+\dfrac{1}{4}\vec{q}$

ということだ。これを$\vec{q}$について解くと、

$\vec{q}=-3\vec{p}+4s\vec{r}$

と③が求まる（キク、ケ）。

次に

$\overrightarrow{FE}=t\vec{p}$であるから

というヒントで、またも$\vec{q}$を表現せよとなっている。$\overrightarrow{FE}$のときは②が道具に使えたが、それに相当するものが今回は与えられていない。

でも、②はもともと前回求めたものなわけで、同じ態度で考えれば$\overrightarrow{FE}$が小文字のベクトルを使ってあらわせればいいよねとなる。

なんで同じ態度をとるのかというと、一回悩んででてきた結果は使いまわしたいし、毎度悩むのはしんどいという思いがあって、悩んだときのものと同じ形をしていれば当てはまるでしょという思惑があるからだ。

これもまた数学以外のときにもある考え方だ。

で、どういう式が作れるかを考えてみると、$\overrightarrow{FE}$の矢印の両端のうち、$F$は小文字ベクトルの始点だからほっとくとして$E$ってなんだっけ？である。この$E$の正体から立式するしか策はないはずで、問題文を読み直すと$a:1-a$に内分する点だったなとわかる。

内分点なので、公式を使って立式が容易だ。

$\overrightarrow{FE}=(1-a)\overrightarrow{FB}+a\overrightarrow{FC}$

と書ける。

これより

$\overrightarrow{FE}=(1-a)\overrightarrow{q}+a\overrightarrow{r}$

と書ける。

ここまでくれば、さっきと同じ状況なので後は手の運動だ。

$t\vec{p}=(1-a)\overrightarrow{q}+a\overrightarrow{r}$

なので、これを $q$について解けば

$\vec{q}=\dfrac{t}{1-a}\vec{p}-\dfrac{a}{1-a}\vec{r}$

と④が求まる（コ、サ、シ）。ここで分母の$a$が$1$だとマズいという議論はあるけど、マーク式においてその検証はもちろん不要だ（ちなみに$a$の範囲から簡単に確認は可能）。

で

③と④により

求めたかったものがついにわかるよとなっている。因果関係で③と④が原因となって結果（答）が求まるということだ。③と④というのは両方とも$\vec{q}$の表現なわけで、一つのものを２通りで表現したことになる。で、これを使えといっているわけで、要は同じってことを使えよと解釈できる。

ベクトルで２つの表現をしたところで、本質的に同じものなわけだから同じ形にしたら同じものになる。

ゆえに、パッと見違うけど、係数も全部同じなはず。ということから、

$-3=\dfrac{t}{1-a}$

だし

$4s=\dfrac{-a}{1-a}$

が成り立つ。

これを解いて、

$s=\dfrac{-a}{4(1-a)}$

$t=-3(1-a)$

と求まる。

（４）次に$\vec{p}$と$\vec{q}$の内積を$a$を用いて表す問題。

①を思い出せとヒントをくれているから、ここで再掲しておこう。

①：$|\overrightarrow{AB}|^{2}=|\vec{p}|^{2}| -2\vec{p} \cdot \vec{q} + \vec{q}|^{2}$

で、今$|\vec{p}|=1$なので、

$|\overrightarrow{AB}|^{2}=1 -2\vec{p} \cdot \vec{q} + |\vec{q}|^{2}$

となる。

なるほど、真ん中に内積$\vec{p} \cdot \vec{q} $が見えている。これを求めるのに邪魔者は$|\overrightarrow{AB}|$と$|\vec{q}|$だ。

そしてこの問題特有の使える武器は、$|\overrightarrow{AB}|=|\overrightarrow{BE}|$である。

次に、$|\overrightarrow{BE}|^{2}$を求める。わからないもののうちの一方である$|\overrightarrow{AB}|$が$|\overrightarrow{BE}|$と同じだよということがヒントなので、$|\overrightarrow{BE}|$の情報を使ってみようということかなと解釈できる。これから既存の右辺$1 -2\vec{p} \cdot \vec{q} + |\vec{q}|^{2}$っぽい形が作れれば（そしてもう一方の未知数 $|\vec{q}|^{2}$を葬り去れれば）等式の変形で答がだせそうだ。

まずは小文字のベクトルの世界に持ってくるために始点を$F$に揃える。

$|\overrightarrow{BE}|^{2}=|\overrightarrow{FE}-\overrightarrow{FB}|^{2}$

$=|t\overrightarrow{p}-\overrightarrow{q}|^{2}=|-3(1-a)\overrightarrow{p}-\overrightarrow{q}|^{2}$

 $=9(1-a)^{2}|\vec{p}|^{2}+6(1-a)\vec{p}\cdot \vec{q} +|\vec{q}|^{2}$

 ここで、$|\vec{p}|=1$なので

 $=9(1-a)^{2}+6(1-a)\vec{p}\cdot \vec{q} +|\vec{q}|^{2}$

と⑥が求まる（ツ、テ）。

これで$|\overrightarrow{AB}|^{2}$が２通りで表現できたから

$1 -2\vec{p} \cdot \vec{q} + |\vec{q}|^{2}=9(1-a)^{2}+6(1-a)\vec{p}\cdot \vec{q} +|\vec{q}|^{2}$

と書ける。

ここまでくれば後は手の運動で

$\vec{p}\cdot \vec{q} =\dfrac{3a-2}{2}$

とわかる（トナ、二、ヌ）。

これで今年のセンターⅡBの問題は一通り終了（最後の確率統計は毎度の通り解いてないけど）。確率統計は、いつか電子書籍化したときのおまけにとっておきたいという思いがあるから（書く日はこないかもだけど）、次回からはまだ解いてない去年のⅡBかな。

ということで、引き続きよろしく。

センター試験過去問研究　数学?・Ａ／?・Ｂ (2019年版センター赤本シリーズ)