
先週は更新をしなかったので、今週は頑張る予定だ(えっへん)。
新しいことを始めようと色々準備してたけど、サラリーマンしてるとなかなか時間がね(言い訳)。
ということで。
ちなみに今更ながらの情報だけど、このサイトはスマホでもいるときもPC版サイトとして見ていただくほうが見やすいのではないかと思う今日この頃。
Latexの関係で、どうしても局所的にスマホ版はいい感じに表示されないので。
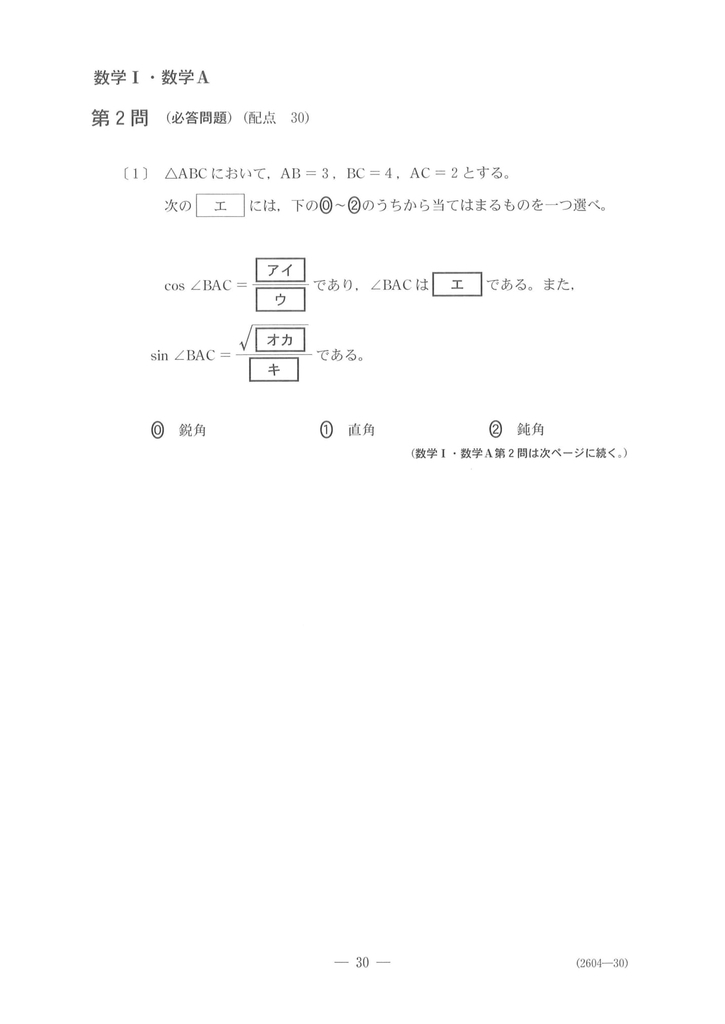
問題
解説
三角比に関する問題。今回図を描くところはおまかせする。
そろそろ学習指導要領のことがわからなくなってきたし、必要ない人がいても知りすぎって程でもないから、適時三角関数という観点を交えながら解説をしたい。
で、まずは余弦定理を知っていますかという問題。公式の解説は過去の記事を参考にしてほしい。
そもそも何故余弦定理を使う気になったのかと問われたならば、そもそも使う動機の主たるところは2つあって
三角形において
・2辺の長さとその挟角がわかっている → 残る一辺がわかる
・3辺の長さがわかっている → 任意の挟角のコサインの値がわかる
といったところだ。
で今回の問題の場合は後者が当てはまる。
公式に当てはめて素直に計算するだけなのでやってみると、
$\cos \angle BAC= \dfrac{3^{2}+2^{2}-4^{2}}{2 \cdot 2 \cdot 3}$
$=\cdots =-\dfrac{1}{4}$
となる(アイ、ウ)。
これがどんな角かというのが次の設問だけど、三角関数の定義を理解していれば瞬殺だ。三角関数ってどう定義されていたかというと、上のリンク先の記事にも書いてるけど、単位円周上(つまり原点を中心とする半径1の円)の点として$(\cos \theta,\sin \theta)$と定義されている。
つまり、今求めた$\cos \angle BAC$は$x$軸上の値のことだとわかる。で、その値が$-\dfrac{1}{4}$だから、負なわけで第2象限にある角=鈍角となる(エ)。
最後に$\sin \angle BAC$を求める。同じ角のコサインがわかっているので、この間の変換は
$\cos^{2} \theta +\sin^{2} \theta =1$
を使うのが常套手段だ。今、角は第2象限にあることからサイン($y$座標)は正であることに気をつけて
$\sin \angle BAC=\sqrt{1-\cos^{2} \angle BAC} $
$= \sqrt{1- \left( -\dfrac{1}{4} \right)^{2}}=\dfrac{\sqrt{15}}{4}$
と求まる。
いつも心に花束を的な感じで、
いつも心に単位円
というのが三角比(三角関数)のポイントだ。
ということで、今回はここまで。

数学が好きな金融サラリーマンが書いたセンター数学?A: 2015年度版 数学が好きなサラリーマンが書いたセンター数学
- 作者: 数学が好きなサラリーマン
- 発売日: 2015/08/24
- メディア: Kindle版
- この商品を含むブログを見る

