8
前回の続き。
実はとても簡単な問題だけど、だからこそバカ丁寧に考えてみる。三角形の面積を求める問題。
問題

解説
(a) 前回色々述べたけど、要は小学校のときからお世話になってる三角形の面積を求めるに過ぎない問題だ。
三角形の面積なんて、まずは底辺と高さをどこに設定するかが肝で、それが難しそうなときに話は広がっていく。
底辺と高さをどこで測るか考えるために、図を描いてみる。
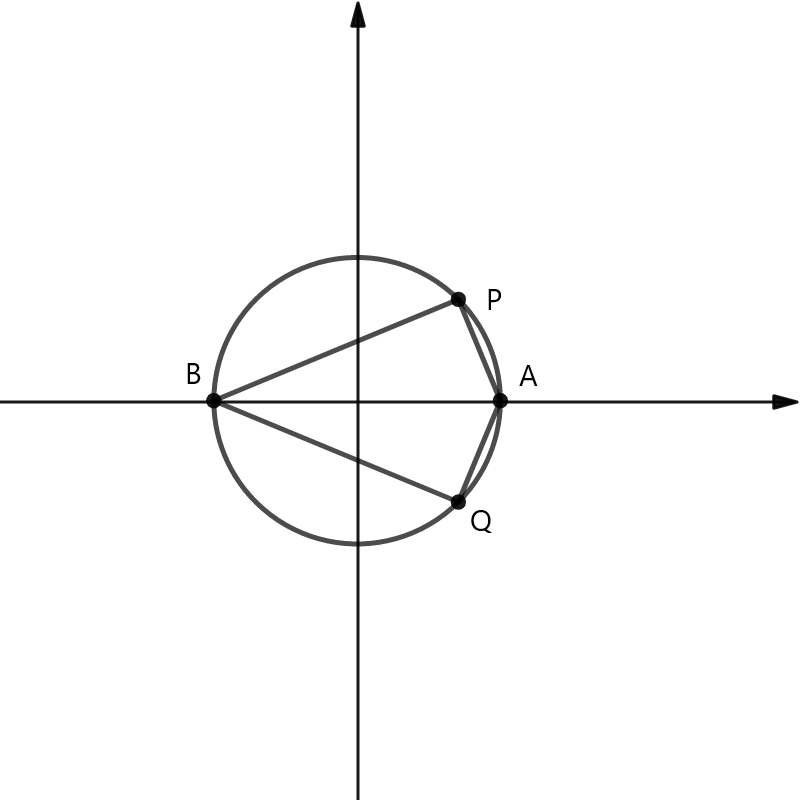
文字の範囲に注意して描いてみたら、迷うことなかれだ。
$\triangle APB$ も$\triangle ABQ$も、底辺は$AB$で、高さは$P$と$Q$それぞれの$y$座標の距離だ。
$|AB|=2$
$P$の$y$座標: $\sin t$
$Q$の$y$座標: $\sin ( \pi + 3t)$
であることから、$\triangle APB$ の面積は
$$ 2 \times \sin t \frac{1}{2} =\sin t$$
$\triangle ABQ$の面積は
$$ 2 \times \left( -\sin ( \pi + 3t) \right) \times \frac{1}{2} = -\sin ( \pi + 3t)=\sin 3t$$
となる。
一つの問題に複数の小問があるときは、誘導であることが少なくないけど、それは還元すると解いた問題は次の問題のヒントということだ。
で、(b)は$S(t)$の導関数を求める問題で、この$S(t)$はもちろん
$S(t)=\triangle APB + \triangle ABQ =\sin t+\sin 3t$
となるので、これを問題文の仰せのままに微分していけばいいわけだけど、この計算はまた次回。

