
問題を解くという行為は、鮮やかに解くということと、泥臭く解くという観点で分けることができる。
一般に鮮やかに解くとは、出題者の意図の通りに解けたときとか、正当に至るまでの経路が短いときのことをいい、泥臭く解くとは、出題者が想定する解法より冗長であったり、ある程度計算量が必要となってしまった場合をいうのだろう。
例えば二次方程式を解くとき、因数分解に気付けた場合、鮮やかに解けたとなり、解の公式を用いた場合、泥臭く解いた、となる。
いずれも「解く」いう点には変わりがなく、スタイルの違いがその形容される語句を分けている。また、多くの人が鮮やかに解けることを期待する一方で、他に選択肢がないような仕方のない局面で泥臭く解を導く。
この泥臭さはときに誤認を生んでいる。
本能的に拒絶反応を起こしてしまうのか、泥臭く解く術を知っているのに「解けない」と判断してしまう。厄介なのは、これを指摘しても、「その解法には気付かなかった」と思ってしまうことだ。泥臭い解法は、その手法があることに気付くこと自体はそんなに難しくないはずだ。
例題として、下掲の図において塗られた部分の面積を考えてもらいたい。
一辺が1の正方形が半径1の扇形が4つ重なることで表されていて、その共通部分の面積である。
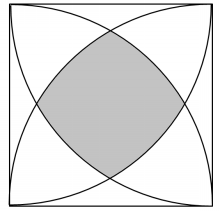
中学数学が好きな方々や文系の方々は、初等幾何を駆使して挑戦したことと察する。解答に辿り着けなかった方もそれなりいるのではないだろうか。
どこかに効果的な補助線を引くことで、鮮やかに解けるのではないだろうかと模索し、あれやこれやとやってみる。ボクはなんだかんだこういったことを考える時間は楽しい。
理系の方で、この問題を解けなかった方にいいたい。あなたはこの図を座標平面上に置き、積分してみることを考えただろうか。
今では、多岐にわたる目的の有益な手段として積分は行われるが、そのもっとも原始的な目的の一つが面積を求めることなのは周知の事実である。
面積とは、単位正方形がその図の中にいくつ入っているのかを示したものである。単純な形においては、初等幾何を用いてそれを計算することが可能なのだが、曲線のようなマス目を数え上げることが極めて困難なものにおいては同様の行為が難しくなる。
そこでかつての数学者たちは、区分求積というギリギリあてはまるマス目からの極限として積分法を使うことに辿り着いた。
この辺の話は理系であれば基本的には知っているべきで、この問題が教科書の積分を習う章の発展問題あたりにあれば、面倒な問題だなと思いつつも素直に解けるはずだ(計算が面倒だから教科書ではないかな)。
おそらく積分が使えなかった理由は、波動拳をゴキブリに使ってしまうようなもったいなさや、積分を使うと複雑になってしまうという予測とかが意識を邪魔して、よもや別単元の手法を用いるとはと思ってしまうことではないだろうか。
つまり、積分を知っているのにこの問題が解けないのは、問題をみたときの初見の印象から初等幾何の問題と判断し、初等幾何の道具のみを使って解こうとしたことにある。
こういったことは、高校の幾何の問題に中学で習う技法を使わないとか、中学の内容に小学生の技を使わないとかにも当てはまる。
基本的に問題を解くとき、自分が知っている知識を制限する理由はない。むしろ、折角有益な道具を知っているのに使わずに、結果解けないのは勿体無いというのを通り過ぎて、情けない気がする。
部屋にゴキブリが出たときに、全力で対処する心意気が大切なのだ。
*ちなみに解答は後日公開。



