【問題解説】センター試験平成31年度本試験ⅠA 第２問－４

 10連休が終わって激務に戻り、はや2週間。次の休日いつだっけとカレンダーをみたら、なんと海の日。。。6月になにか休日が欲しいところ。

ということでセンター解説続編。

問題

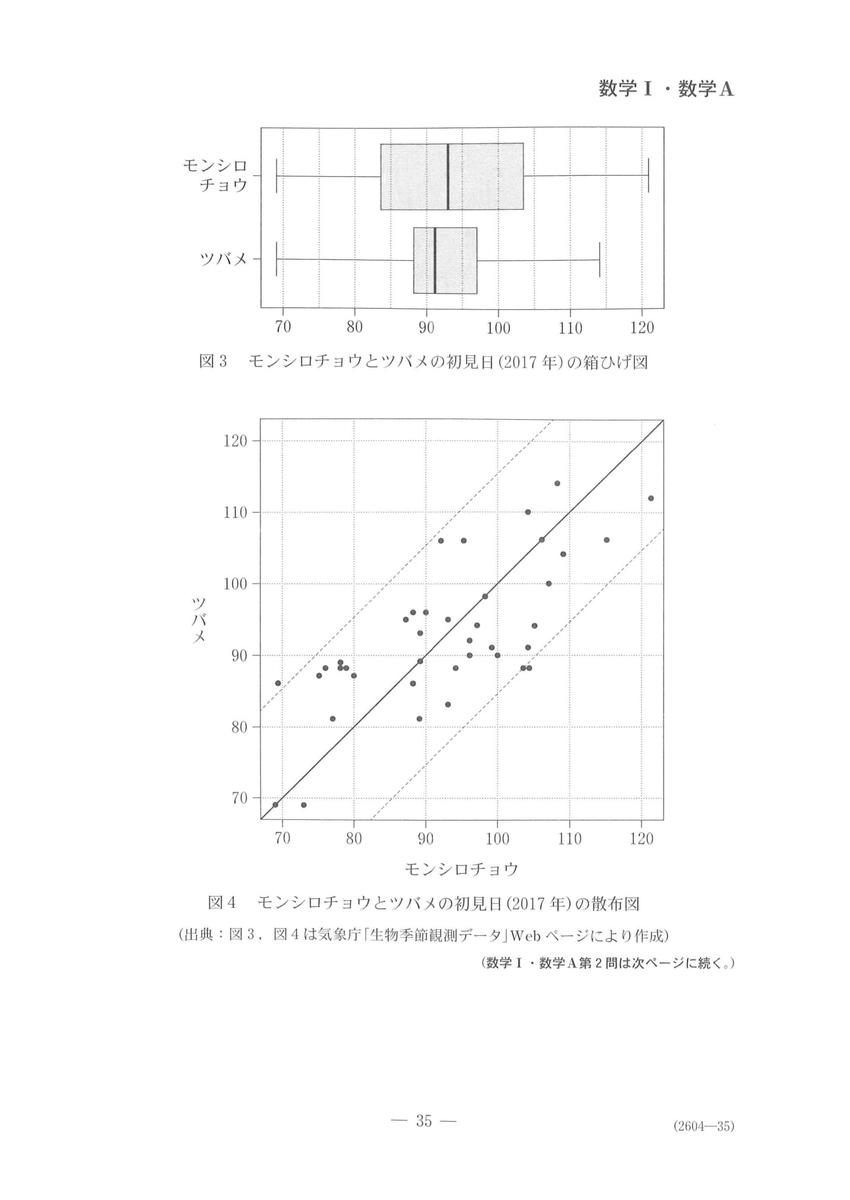
解説

なんだか数学らしくない感じが毎度するこの分野の問題。腐らずちゃんと文章を読んで解いてみる。

正しくないものを選べという表現になっているけど、否定表現って頭の中でワンクッション挟んでしまいがちだ。ここを肯定表現にしておくと、間違っているものを選べということになる。

この観点を忘れずに上から順番にみていこう。

問題では２つの図が与えられている。どちらも基本的なもので、特に散布図の方は直線を付加しておいたと問題文は言っている。この付加されたものがどんな役割をもつのかは意識しておきたい。真ん中に置かれた$y=x$（傾き１の直線）は何を表しているのだろう。

一般に数学（以外のところでもそうなんだけど）において、

定量的扱い

と

定性的解釈

は重要な観点だ。数字は何を語り、森羅万象はどう数字化できるのか。小学校のときの文章題の問題とは、まさにこの定量化ということの入門編なわけだし、百分率は数値から様々な定性的傾向を汲み取る手段として重宝される。ボクらは定量と定性のあいだを生きている（冷製と情熱のあいだにかけてみたけど、全然うまくなかった）。

 そしてこの問題でも、定量的に与えられた$y=x$（傾き１の直線）があって、設問は定性的なものが多いわけだから、その解釈を意識するということはとても自然なことなわけだ。

直線とは点の集合であり、それが$y=x$という関係でプロットされているということを考えれば、直線上の点はモンシロチョウとツバメの初見日が同じものと解釈できる。同じ考え方で、切片が異なるということは、切片が15である直線は

$y=x+15$

の式を満たす。もう少し見やすい形にすると、

$y-x=15$

となって、同一地点のツバメの初見日とモンシロチョウの初見日の差が15日であることがわかる。

で、そもそも。どういうときにどっちの図を見ればいいのだろうか。身も蓋もない言い方をすれば、答が判断できる方・しやすい方を使えばいい（いや、本当に身も蓋もないな）。片方でしか判断できないこともあれば、両方から答えられそうなものもある。ここで抑えておくべきは、箱ひげ図はデータの並びに対する特徴が見やすい図だけど、ポイントとなる箇所の値しか読み取りにくいし、分布図は箱ひげ図より素データに近いけど、削がれていない分だけ情報が多い。この辺を前提に選択肢をみていこう。

ということで、０から。

０：

最大値とか最小値は箱ひげ図で表される特徴ある点なので、箱ひげ図を使ってもいいし、分布の状況からも判断できる。箱ひげ図からわかることは、箱ひげ図を使った方が手っ取り早い。

とはいえ、箱ひげ図は図下に置かれている数字上に最小値がないと、同じようなところにあるなとは思えても、ほんとに同じ位置なのか迷ってしまう。

ゆえに分布図を眺めてみる。最小値は、その名の通り最も小さい値だからそれぞれの軸で一番小さい点が、同じ日($y=x$上）にあればよくて、実際あるので正しいとわかる。

１：

最大値比べで、０の最小値と異なってどっちが大きいかの比較なので、箱ひげ図で判断が簡単にできる。

あえていうならば、ここでは文の読み間違いに気をつけたい。

モンシロチョウの初見日の最大値はツバメの初見日の最大値より大きい。

どちらの初見日が大きければ正しいと言えるのか普通に読めばなんてことないけど、試験とかの特別な状況下ではケアレスミスで誤判断してしまうこともあるはずだ。

そんなときボクは、主部と述語のみをかいつまむ’（表現これでいいんだっけ）。つまり

モンシロチョウの最大値は、大きい

と読む。するとモンシロチョウの初見日の最大値が大きいのか否かをみればいいとわかって、箱ひげ図は確かにそれを示しているので、正しいとわかる。

２：

次は中央値。中央値は、データを一列に並べたときの中央にくる値で、分布から見抜くのは困難だ（数えればできるんだろうけど）。これも箱ひげ図なら、箱の中に引かれた線を見るだけなので、簡単にわかる。モンシロチョウの中央値が大きいので、これも正しい。

３：

中央値同様、四分位範囲も箱ひげ図が圧倒的に見やすい。

目盛り幅が５であることを前提に、モンシロチョウは目盛り幅が３つ分入っているのと、両端はみでた分が丁度１目盛り幅分と捉えると、

$5 \times 4 = 20$

が四分位範囲だ。

ツバメの四分位範囲は同じようにカウントすれば小さく見積もって１．５幅分くらいなので

$5 \times 1.5 = 7.5$

となる。

 するとツバメの３倍との比較なので

$7.5 \times 3=22.5>20$

なので正しい。

４：

１５日は目盛り３つ分で、モンシロチョウの四分位範囲は目盛り３つ分を内包しているのは箱ひげ図が示しているとおりなので、間違っている＝正しくない。

５：

ツバメの四分位範囲は大きく見積もっても目盛り３つ分もないので、正しい。

６：

モンシロチョウとツバメの初見日が同じということは、冒頭の考察の通り$y=x$にある点として、分布上で示される。なので直線上の点を数えればよくて、確かに４つ確認できる。問題文は、分布全体で２個重なった点があるといっているので、少なくとも４つあるというのは正しい。

７：

正しくない選択肢が今のところ一つしかないので、消去法的にこれが正しくないということになる。といって終わるのもアレなので、ちゃんと考察しておこう。

といっても、冒頭の考察の通り、$y=x \pm 15$の直線は,

$y-x= \pm 15$

と移項すれば明らかで、同一地点における初見日の差が１５日であることを示すものだ。ということは、これらの直線の外側にある点は１５日以上なわけで、分布図をみるとたしかにそういう点はあるので、この選択肢は間違っている＝正しくない。

用語の意味を知っていれば超簡単なこの分野。でも、こういう図表を読み解く問題の解法というのは、他の教科でも役に立つのかな（適当）。

今回はここまで。

センター試験過去問研究 数学I・A/II・B (2020年版センター赤本シリーズ)

大学入試センター試験過去問レビュー数学1・A,2・B 2020 (河合塾シリーズ)

大学入試センター試験過去問題集数学1・A,2・B 2019 (大学入試完全対策シリーズ)