【問題解説】センター試験平成30年度本試験ⅡＢ 第１問－２

台風24号が強烈で夜中ビクビクしていたせいで、とても寝不足な今日。頑張って一週間働けば、週末は連休だ。頑張ってこう。

ということで、前回の続き。

空欄補充系の問題って、目の前の一つずつを片付けていこうという意識が働くときがある。すると全体として何やってるんだっけ？というところがおろそかになって、結果誘導にうまく乗れないなんてことになることがある。

こういうことをいうと、「なるほど。しっかり問題文を読もう」と思ってくれる人がいて、それはそれでありがたい話なのだが、そもそもしっかり読むって何よ？と実は心の中では感じてたりもしている。

ボクの大学受験勉強時の初期もそうだったんだけど、しっかり読むってことを繰り返しゆっくり問題文を読むことなんて勘違いしている人ってそれなりにいるのではないだろうか。

しっかり読むとは、読む対象によっても多少定義は変わるのだろうけど、こと大学受験数学の問題においては、何が問われて、何を与えられているのか（条件とヒント）ということを整理することに尽きる。

短い問題においてはそれは明白なのだが、今回のような比較的長い文章で書かれた問題だとそういう観点があいまいになる。まぁ、あいまいでも問題が易しければ大したことはないのだけど。

で、この問題をしっかり読んでみると、

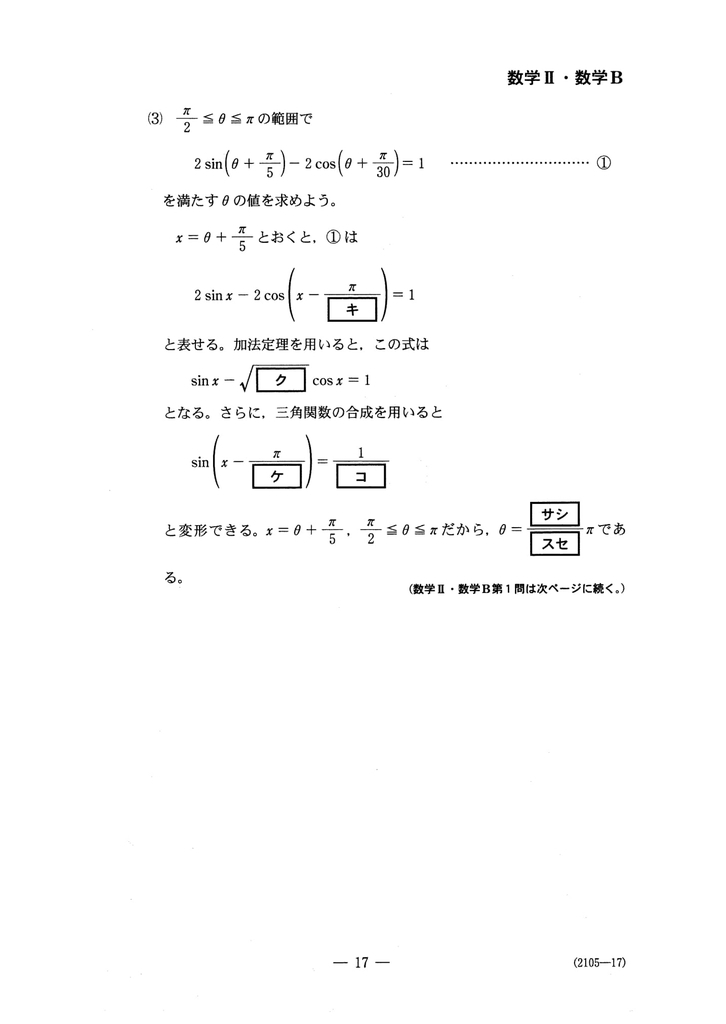
何が問われているのか︰
①の式での　$ \theta$
何を与えられているのか（条件）︰
$\dfrac{\pi}{2} \leqq \theta \leqq \pi$
何を与えられているのか（ヒント）︰
1. $x=\theta + \dfrac{\pi}{5}$ とおくこと。
2. $x$で表した式に加法定理を用いるとイイコトがある。
3. 2.の式に三角関数の合成を使うと更にイイコトがある。
4. $x=\theta + \dfrac{\pi}{5}$ とおいたこと、$\dfrac{\pi}{2} \leqq \theta \leqq \pi$が与えられていることから答えが求まること。

という情報が得られる。問題の流れを見失ったときはいつでもここに戻ってこよう。

キから順番に考えていくと、まずは

 $x=\theta + \dfrac{\pi}{5}\   \Leftrightarrow \  \theta=x-\dfrac{\pi}{5} $

 を代入するだけなので

$ 2\sin x-2\cos \left\{ \left( x - \dfrac{ \pi }{ 5 } \right) + \dfrac{ \pi }{ 30 } \right\} = 1 $

$\Leftrightarrow 2\sin x-2\cos \left( x - \dfrac{ \pi }{ 6 } \right) = 1 $

と簡単に求まる。

ここで問題で使おうが使いまいが、新しい変数（今回の場合、$x$）を持ち込んだときに常に考えておきたいことがある。

それは文字変数がでてきたとき、その定義域はどういう範囲かということだ。特に、今回のようにある文字を別の文字で置き換えるようなとき（今回は$\theta$を$x$に置き換え）、元の文字の定義域を変形しつつも引き継ぐ。さながら、虎は死んで革残すの状況だ（変数は死んで、変域残す？）。

具体的に考えてみると、$\theta$は

$\dfrac{\pi}{2} \leqq \theta \leqq \pi$

の範囲を動く。$\theta$に$ \dfrac{\pi}{5}$加えたものが$x$なので、

$\dfrac{\pi}{2} +\dfrac{\pi}{5} \leqq \theta +\dfrac{\pi}{5} \leqq \pi +\dfrac{\pi}{5}$

 $\Leftrightarrow \dfrac{7 \pi}{10} \leqq x \leqq \dfrac{6 \pi}{5}$

 となる。

続いて、$x$で表した式に加法定理を使うことを問題は教えてくれている。

加法定理（$\cos$の中身が差の場合）

$\cos (\alpha -\beta)=\cos \alpha \cos \beta + \sin \alpha \sin \beta$

 これを問題分の適用できる方の項$\cos \left( x - \dfrac{ \pi }{ 6 } \right) $にあてはめると

 $\cos \left( x - \dfrac{ \pi }{ 6 } \right) =\cos x \cos \dfrac{ \pi }{ 6 } + \sin x \sin \dfrac{ \pi }{ 6 }$

ここで$\cos \dfrac{ \pi }{ 6 } = \dfrac{ \sqrt{3} }{ 2 }$、$\sin \dfrac{ \pi }{ 6 } = \dfrac{ 1 }{ 2 }$なので、

$ =\dfrac{ \sqrt{3} }{ 2 }\cos x+\dfrac{ 1 }{ 2 }\sin x$

 となる。よって

$2\sin x-2\cos \left( x - \dfrac{ \pi }{ 6 } \right) = 1 $

$\Leftrightarrow 2\sin x-2 \left( \dfrac{ \sqrt{3} }{ 2 }\cos x+\dfrac{ 1 }{ 2 }\sin x \right) = 1 $

$\Leftrightarrow \sin x - \sqrt{3} \cos x =1$

 となり、クは$3$とわかる。

さて。ここまではただ目の前の計算をしただけで求まる。ここで考えたいのは、この問題文はなぜ$x=\theta + \dfrac{\pi}{5}$ と変数をおき、加法定理を使えと誘導してきたのかだ。

①の式での$ \theta$を求める為に、この行為はどう役に立つのだろうか。

複雑な問題では、まず単純化して考えることは王道的解決方法だ。①の式から$ \theta$を求める問題と同じ種類のシンプルなものを考えてみる。

シンプルに考えるということは、何をしているかの究極的要素だけを抽出することにほかならない。この問題は何を問うているかというと、

三角関数で与えられた式から角度

だ。

例えば、

$\sin $□ $=$■

という式で■の値が具体的にわかっているときの□を求めるという行為だ。

でもこれって、よくよく考えるとどんな■でもボクらは□を求められるなんてことはない。具体的にみてみると、

$\cos \theta=\dfrac{\sqrt{3}}{2} \ \left( 0 \leqq \theta \leqq \pi \right)$

は

$\theta=\dfrac{\pi}{6}$

と求められるが

$\cos \theta=\dfrac{1}{3} \ \left( 0 \leqq \theta \leqq \pi \right)$

 となると？？となる。ボクらは有名角かその組み合わせで表現されていないと、その角度を言い当てることはできないし、

$\sin $□ $=$■

みたいなシンプルな形にしておかないとその言い当てる行為すら難しい。

ということは、逆算的に考えると、ボクらは

$\sin $□ $=$■

の形に持ち込む方法を考える必要がある。問題文は、この行為に合成を用いよと教えてくれているわけだ。確かに合成しか方法がなさそうだ。

ということで、合成できるような方向に持っていきたい動機ができた。合成というのは加法定理の逆操作だから、係数に有名角が出てきてくれないと計算ができない。

$x=\theta + \dfrac{\pi}{5}$とおくことで $\dfrac{\pi}{5}$なんて有名でない角を除外できるし、現れた$\cos \left( x - \dfrac{ \pi }{ 6 } \right) $に加法定理を使うことで係数に合成するに都合のいい狙いの値がでてくることを示唆してくれている。

実際に合成の計算をしてみよう。

$\sin x - \sqrt{3} \cos x =1$

$\Leftrightarrow \dfrac{1}{2} \sin x - \dfrac{\sqrt{3} }{2} \cos x =\dfrac{1}{2}$

$\Leftrightarrow \cos \dfrac{\pi}{3} \sin x - \sin \dfrac{\pi}{3}  \cos x =\dfrac{1}{2}$

 ここで加法定理の逆を適用して

$\Leftrightarrow \sin \left( x- \dfrac{\pi}{3} \right) =\dfrac{1}{2}$

となる。よって、ケは$3$だし、コは$2$になることがわかる。

ここで、狙いの

$\sin $□ $=$■

の形になったので、その角度を言い当てることにしよう。

さっき

$ \dfrac{7 \pi}{10} \leqq x \leqq \dfrac{6 \pi}{5}$

は求めておいた。これに$\dfrac{\pi}{3} $をひいたものが□で、そのときの■が$\dfrac{1}{2}$ということになる。

$ \dfrac{7 \pi}{10} -\dfrac{\pi}{3} \leqq x -\dfrac{\pi}{3} \leqq \dfrac{6 \pi}{5} -\dfrac{\pi}{3}$

$\Leftrightarrow \dfrac{11 \pi}{30} \leqq $ □ $ \leqq \dfrac{13 \pi}{15}$

で、この範囲の□に対して

$\sin $□ $=\dfrac{1}{2}$

を求めればいい。これは

□$＝\dfrac{5 \pi}{6}$

になる。ゆえに

$x -\dfrac{\pi}{3} ＝\dfrac{5 \pi}{6}$

$\Leftrightarrow x  ＝\dfrac{5 \pi}{6} + \dfrac{\pi}{3}=\dfrac{7\pi}{6}$

 $x=\theta + \dfrac{\pi}{5}$ だったから

$\theta=x-\dfrac{\pi}{5}=\dfrac{7\pi}{6}-\dfrac{\pi}{5}=\dfrac{29}{30} \pi$

となる。

ちなみに、三角関数とはいうものの、定義には注意しておきたい。

三角関数の定義

半径1の単位円において、$(1,0)$から原点中心に$\theta$回転したときの座標で、

$x$座標が$\cos \theta$

$y$座標が$\sin \theta$

となる 。

 $0 \leqq \theta \leqq \dfrac{\pi}{2}$のときは三角形で定義されるけど、一般には円で定義されていることはとても重要な事実だ（故にときに円関数とも呼ばれる）。

---

今回はここまで。

数学が好きな金融サラリーマンが書いたセンター数学?A: 2015年度版 数学が好きなサラリーマンが書いたセンター数学

数学が好きな金融サラリーマンが書いたセンター数学?B: 2015年度版 数学が好きなサラリーマンが書いたセンター数学