久々にコラムを書こうと思ったけど、やっぱり今回も解説の方で。
今回から確率です。同様に確からしいものを分母にするってのが、わかってるようで案外理解が難しいところです。
特に条件付確率あたりは顕著で、感覚的に確からしいよねなんて捉えると罠にはまります。例えば子どもが二人いたとして、一方が男で火曜日に生まれたとき、ふたりとも男である確率と、火曜日に生まれたなんて情報がない条件下でふたりとも男である確率って異なるんです。
ゆえにオススメな考え方はふたつで
- すべてのパターンを数え上げることからはじめる(すべてのものを区別して数える)
- 素直に公式に当てはめて求める
です。
大したことじゃなく見えますが、ここを怠ると罠にハマります。
面白いけど、罠がある。罠があるから、面白い。そんな分野だと思います。 興味ある人は下記の記事もご参考のほど。
【コラム】モンティ・ホール問題をいま一度 - 数学が好きなサラリーマンのブログ
【問題解説】最短経路の確率問題の罠 - 数学が好きなサラリーマンのブログ
ということで問題です。
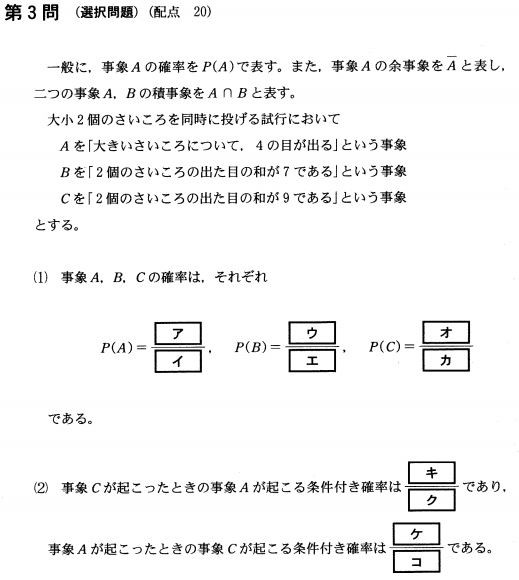
(1)
こういう問題をみたときに、すべてのパターンを拾うという観点で、例えば縦に大のさいころ、横に小のさいころの目を下記並べた総当たり表を書き始める人がいると思います。
別に悪くはないのですが、事象を座標平面上に展開できるようなスタイルにしておくと何かと応用がききます。この問題では
(大のさいころの目、小のさいころの目)
と表現することにします。
$P(A)$から順番に考えていくと、これは大きいさいころについて4の目が出る事象の確率です。ということは(4, ☆)という形になる確率です。
(★, ☆)のパターンは全部36通りあって、(4, ☆)となるのは☆が1~6の6通り。ゆえに
$
P(A)=\dfrac{6}{36}=\dfrac{1}{6}
$
です。
次に$P(B)$で、2個のさいころの出た目の和が7となる事象の確率です。地道に数え上げることが基本です。足して7となる数の組み合わせで、
(1, 6)
(2, 5)
(3, 4)
(4, 3)
(5, 2)
(6, 1)
です。よって
$
P(B)=\dfrac{6}{36}=\dfrac{1}{6}
$
です。まぁ7なので、すべての目に相方がいるのはそりゃそうよねって感じです。
$P(C)$は、2個のさいころの出た目の和が9となる事象の確率です。考え方は同じで、
(3, 6)
(4, 5)
(5, 4)
(6, 3)
のときなので、
$
P(C)=\dfrac{4}{36}=\dfrac{1}{9}
$
となります。
(2)
条件付確率を求める問題です。確率論はギャンブルに端を発したということもあって、数学の中では生活感覚に近いところにある学問です。ゆえに定量的に評価された結果の値を定性的な目線で解釈する、ということはありがちです。例えば、このギャンブルに勝てる確率は8割ですと確率値がわかれば、結構勝てるのね、賭けてみるかななんて思うわけです。
ここまではそれでいいと思うんですが、ポイントはこの定性的見解が確率計算よりも先んじてしまうことがあります。冒頭で話した
子どもが二人いたとして、一方が男で火曜日に生まれたとき、ふたりとも男である確率と、火曜日に生まれたなんて情報がない条件下でふたりとも男である確率って異なるんです。
がその例です。一方が火曜日に生まれようが生まれまいが、性別の判断に関係ないよねと思いがちです。でも実のところ火曜日に生まれたという情報によって確率は変動します。
そりゃ確率は低くなるだろと直感的に思える人は別ですが、感覚的に考えると気付かず罠にハマってしまうことがあるんです。
こういうときに、じゃ罠に気づけるようになろうと思うことは間違っています。計算ミスをしやすい人が、気をつけて計算しようという決意をするのと似ています。計算ミスをしやすい人はもちろんわざとミスってるわけではありません。無意識なんです。だから、無意識にやることをコントロールするなんて難儀なわけです。
ではどうするかというと、計算ミスをしないようにではなく、ミスしても大丈夫な手だてを高じておくわけです。例えば毎度検算するとか。同じ話で本筋に戻れば、罠に気づけるようにするのではなく、罠にかかっても問題ないようにするということです。つまり、感覚的なところでは誤解しても、計算上は正しく求められるようにするということです。そしてそれは公式を用いるということです。
え?と思った人。気持ちわかります。確率において、感覚と事実のずれというのは、すなわち同様に確からしい全パターンの認識のずれです。上の例でいうと、二人の子供の情報を(曜日, 性別, 曜日, 性別)と表現することにして、すべてを$7 \times 2 \times 7 \times 2=196$通りでとらえる必要があります。これを感覚的には、火曜日って関係ないんじゃね?というキモチで(性別, 性別)で考えて4通り(確率は、(女, 女)を除いたところで(男, 男)の確率だから$\dfrac{1}{3}$)と考えてしまうわけです。 手に入れた情報(曜日)を無駄にしないという姿勢が肝なんですが、そして入試問題では無駄な条件なんてないってのが基本ではあるのですが、この辺(全パターン)を理解できていないと違和感でばかりを抱いてしまいます。
そんなときには潔く公式を頼りましょうってのが手っ取り早いです(毎度全パターンからの考察も当然ありですが)。今回はセンター問題解説なので細かい計算は省略しますが、条件付確率の公式に放り込むと、
$\dfrac{13}{27}$
と求まります。ゆえに条件付き確率だってわかることがまず何よりです。
そんなこんなで、ほかのジャンルに比べて面白い特徴をもつ確率問題ですが、センターの問題はとても簡単です。そして条件付き確率であることも教えてくれています。
まず事象Cが起きたときの事象Aが起きる条件付き確率$P_C (A)$です。公式にそのまま当てはめて
$
P_C (A)=\dfrac{P(A \cap C)}{P(C)}
$
ここで$A \cap C$は、(1)で書き並べたCの要素で大きいさいころが4の目のものは(4, 5)だけなので$P(A \cap C)=\dfrac{1}{36}$です。ゆえに
$
\dfrac{P(A \cap C)}{P(C)}=\dfrac{\frac{1}{36}}{\frac{1}{9}}=\dfrac{1}{4}
$
となります。ちなみにこの問題の場合は、感覚的に考えると和が9となるときに大きいさいころが4の目となる確率は明らかに小さいさいころが5のときだけが対象なので$\dfrac{1}{4}$となり計算と合致します。
最後に今の逆の$P_A (C)$を求めます。これも公式に当てはめて
$
P_A (C)=\dfrac{P(A \cap C)}{P(A)}=\dfrac{\frac{1}{36}}{\frac{1}{6}}=\dfrac{1}{6}
$
となります。ちなみにこの問題の場合も、感覚的に考えると大きいさいころが4の目のときに和が9となる確率は明らかに小さいさいころが5のときだけが対象なので$\dfrac{1}{6}$となり計算と合致します。
両方とも公式を振りかざさずとも解けてしまうので、優しすぎて魅力半減な感じがします。。モッタイナイ。 今回はこの辺にて。

数学が好きな金融サラリーマンが書いたセンター数学?B: 2015年度版 数学が好きなサラリーマンが書いたセンター数学
- 作者: 数学が好きなサラリーマン
- 発売日: 2017/08/26
- メディア: Kindle版
- この商品を含むブログを見る

数学が好きな金融サラリーマンが書いたセンター数学?A: 2015年度版 数学が好きなサラリーマンが書いたセンター数学
- 作者: 数学が好きなサラリーマン
- 発売日: 2015/08/24
- メディア: Kindle版
- この商品を含むブログを見る

