【問題解説】センター試験平成30年度本試験ⅡＢ 第３問－２

仕事で、

これは前任者がとても苦労したタスクで複雑で時間がかるけど、今年これを引き継いでくれないか。

とアサインされることがある。早めに取り掛かると少しは楽だよなんてヒントもくれるけど、誰かがすでに苦労したならそれが無駄にならないようにパッケージ化するとかその人の努力に報いてあげないと、会社は進歩しないよと考える今日この頃。

でもこれって人生もそうだよね。おじいちゃんの人生で得たものを孫にインストールできれば学校の授業は情報のアップデート＋αになって短縮できるはず。

ということで前回の続き。

問題

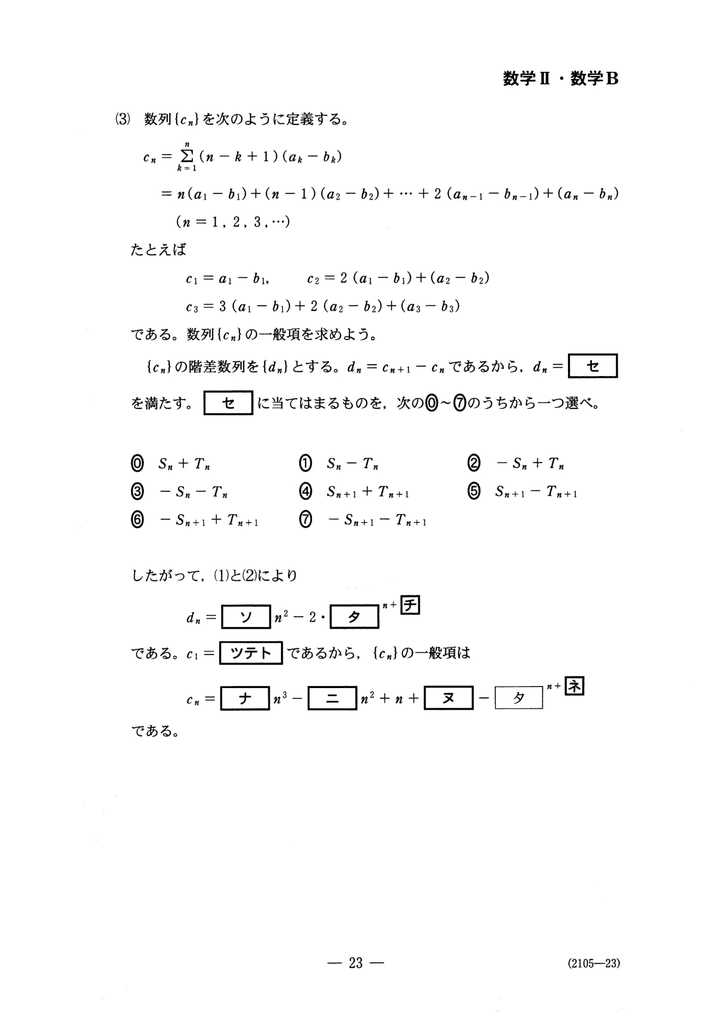
 解説

（３）$c_{n}$が少し面倒な形で与えられている。ここでは、王道的な解き方は他に譲って、マークシート的な観点を活用しながら解いてみたい。

まずは、$c_{n}$の階差数列$d_{n}$を、前問で求めた等差数列と等比数列それぞれの和、$S_{n}$と$T_{n}$で表す問題だ。

マークシート的な観点とは、必要と十分の関係に着眼することだ。ボクらは数学において、『一般に』成り立つかどうかを兎角扱うが、マークシートにおいて解の十分性までを問うことは難しいから、必要条件である『具体的な』値が成立するということだけで問題が解けてしまうことがある。

つまり、一般に$n$での成立を考えなくても、具体的な$n=1$とか$n=2$など値を代入したところで成り立つことが利用できるということだ。

とはいえ、マークで問われているところ次第で有効かどうかが分かれるので、これだけですべてを解ききれるとは限らない。適宜、状況を見極めながら判断していこう。一つの判断材料として、一つの式にいくつも未知数（マーク箇所）があるものには向いていない。

 で、最初の$d_{n}$の形だけど、$n=1$とか$n=2$を代入することを考えてみると、選択肢はすべて$S_{1}$とか$T_{1}$、もしくは$S_{2}$とか$T_{2}$になる。それぞれ和の形は求めているから簡単に値はわかるわけで、$d_{1}=c_{2}-c_{1}$も等差数列と等差数列のはじめの方の項を使って計算するだけだ。大した事なさそうなので、代入を試みてみることにする。

前回の問題で、

$a_{1}=-6$

$a_{n}=12n-18$

$b_{1}=12$

$b_{n}=12 \cdot 3^{n-1}$

はわかっている。これらから、「たとえば」と問題で例示してあるものは容易に求まる。

$a_{2}=24-18=6$

$b_{2}=12 \cdot 3=36$

$a_{3}=36-18=18$

$b_{3}=12 \cdot 3=36$

$c_{1} = a_{1}-b_{1}=-6-12=-18$（ツテト）

$c_{2}=2(a_{1}-b_{1})+(a_{2}-b_{2})=2\cdot(-18)+(6-36)=-66$

$c_{3}=3(a_{1}-b_{1})+2(a_{2}-b_{2})+(a_{3}-b_{3})$

$=3\cdot(-18)+2\cdot(-30)+(18-36)=-132$

ここで我々の目的は何だったかというと、$d_{n}$がどんな形で表されるかであって、マークシート的な観点からいえば、$d_{1}$や$d_{2}$あたりの値と一致するものはどれかということだ（例示されたものからわかるのは$d_{1}$と$d_{2}$）。

でそれぞれの値を計算してみると、

$d_{1}=c_{2}-c_{1}=-66-(-18)=-48$

$d_{2}=c_{3}-c_{2}=-132-(-66)=-66$

なので、こういった値になるものを選択肢から探してみる。

選択肢で使う$S_{1}$や$S_{2}$と、$T_{1}$や$T_{2}$も計算しておく。

$S_{1}=a_{1}=-6$

$S_{2}=a_{1}+a_{2}=0$

$T_{1}=b_{1}=12$

$T_{2}=b_{1}+b_{1}=48$

 前回求めた和の式に代入してもいいんだけど、するまでもなくこれらの値がわかる。

で選択肢の式の値を考えてみる。全部に代入してみてもいいけど、$d_{1}=-48$とそれなりに大きい値なのに対し、$S_{1}=-6$と$T_{1}=12$の組み合わせではまるで届かないのは明らかなので、$S_{2}$と$T_{2}$の組み合わせの中に答はある。とはいえ、$S_{2}=0$なので、符号に着目して⑤か⑦であることまではわかる。

ここで今度は$d_{2}=-66$であることを使う。⑤と⑦だけを考えればいいわけで、

$S_{3}=S_{2}+a_{3}=18$

$T_{3}=T_{2}+b_{3}=48+36=84$

であることから⑤が成立することがわかる。

次に$d_{n}$の一般項を求める。これは問題が$d_{n}$を何故⑤の形で表現できることを教えてくれたかと考えると、そりゃ前回$S_{n}$と$T_{n}$を求めたから、代入するだけで正体が明らかになるようにだよねってなる。

とはいえ。ここで律儀に代入して計算するのはもったいない。

$S_{n}=6n^{2}-12n$

$T_{n}=6(3^{n}-1)$

を$n \rightarrow n+1$として差をとればいいんだけど、 $n^{2}$の係数6は変わりようがないし、指数パートのところも3で計算結果変わらないことは容易にわかる（つまり、ソは6、タは3）。ということは、この問題で問われているところはチだけだ。で、$d_{1}=-48$はわかっているわけだから、

$d_{1}=6 \cdot 1^{2}-2\cdot 3^{チ+1}=-48$

となる。これを解いて、チは2とわかる。

最後に$c_{n}$を考える。これは変数がナ、ニ、ヌ、ネと4つもあるので変数とおいて今まで同様代入計算で解くのはしんどいから正面から考えてみよう。

そもそもこの問題は、最初に$c_{n}$の一般項を求めようと宣言した後で階差数列$d_{n}$が登場している。

ということはつまり、一般項を求めるのに階差数列が使えるよということだ。

ここで一つ、階差数列とは何たるかを確認しておきたい。各項の差をとったものでしょと思うかもしれないが、それ以上の役割がある。

数列は一般に自然数を変数とする関数とも解釈できる。もちろん、自然数ゆえにトビトビの値で連続でないから微分や積分の計算は不可能だ。

しかし、それぞれに呼応する表現が存在する。それが階差数列と数列の和である。

階差数列は

$\frac{a_{n+1}-a_{n}}{(n+1)-1}$

と書けば変化量を表す式だし、

数列の和と積分はそれぞれ総和という共通点がある。

そしてさらに、微分された関数を積分するともとの関数の形がわかるように、階差数列の総和を取ることで元の数列の形が見えてくる。つまり、

$\displaystyle c_{n}= c_{1} + \sum_{k=1}^{n-1} (c_{k+1}-c_{k})$

となる。

微積分との関係の考察はここではこれ以上には広げないが、微積分での扱いと同じような態度を取ることが出るということだ。

 導関数的立ち位置の階差数列がわかっているので、積分するキモチで和をとって、

 $\displaystyle c_{n}= c_{1} + \sum_{k=1}^{n-1} (c_{k+1}-c_{k})$

$\displaystyle = c_{1} + \sum_{k=1}^{n-1} b_{k}$

$\displaystyle = c_{1} + \sum_{k=1}^{n-1} (6k^{2}-2\cdot 3^{k+2})$
$=-18+6\cdot \dfrac{(n-1)n\{2(n-1) +1\}}{6}-2\cdot \dfrac{3^{3}(3^{n-1}-1)}{3-1}$

$=2n^{3}-3n^{2}+n+9-3^{n+2}$

と求まる（ナ、ニ、ヌ、ネ）。

 たまにはこんな解き方もね。 

今回はここまで。

センター試験過去問研究　数学?・Ａ／?・Ｂ (2019年版センター赤本シリーズ)