【問題解説】センター試験平成30年度本試験 IA　第2問 (2) - 数学が好きなサラリーマンのブログ

間が空いてしまいましたという始まりが常套句になってきました。久々の更新です。データの分析の問題ですが、相変わらず問題文は長いのに、中身は簡単です。これだけの前振りでこれだけかよみたいな。これはもはや国語や社会の問題ではないだろうか（つまり数学ではない）と思いつつ、悪口はこの辺にして問題解説します。

f:id:mathbanker:20180417174111j:plain

f:id:mathbanker:20180417174127j:plain

選択肢を上から順に検討していきます。答えが判明した地点で終了ではありますが、一応最後の選択肢まで考えてみます。ちなみに以前にも紹介しましたけど、図表をみて判断なんてときに我々が取れる態度は決まっています。 特異な点に着目するか、全体的な傾向をみるかです。ミクロにみるときは存在するものを探し、マクロにみるときには傾向を考えます。

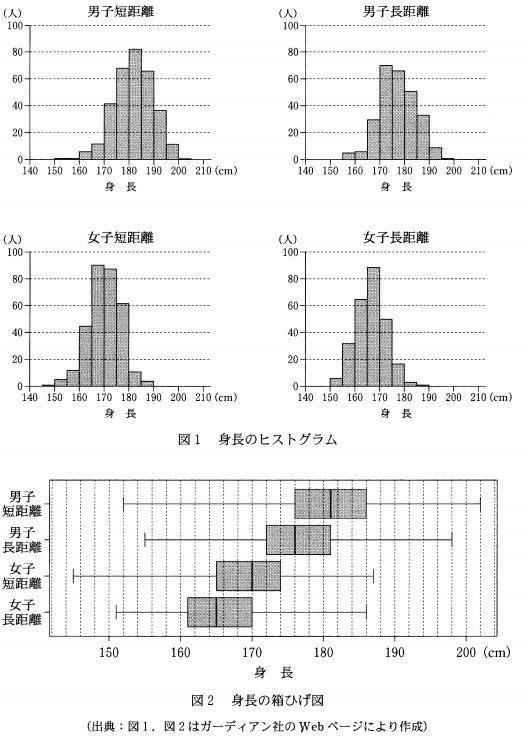
0：範囲が最も大きいのが女子短距離グループだと選択肢はいっています。女子短距離グループの範囲を数値で捉え、それより大きいものが存在していないか確認します。グラフはヒストグラムと箱ひげ図があるので、どっちを使うかを判断する必要があります。 範囲の広さを考えたいわけですが、ヒストグラムは階級で考えるので、階級には幅があることから厳密な勝負になったときにどちらが優勢かわかりません。一方箱ひげ図は最大値と最小値が表現されているので、ヒストグラムより厳密に検討が可能です。

ということで、箱ひげ図を使います。まず女子の短距離グループの範囲を考えると、最大値187、最小値145になります。ということで範囲は187ー145＝42です。これが基準で、これより大きいものがあれば選択肢は不成立、なければ成立となります。

男子短距離グループは、最大値202最小値152なので、範囲は202ー152＝50です。もうありました。これで女子短距離グループは範囲が最も大きいとは言えません。

1：これは4つのグループの四分位範囲を実際に検証してみればわかります。四分位範囲がすぐにわかるのは箱ひげ図です。各区切幅が2なので、幅何個分が四分位範囲に含まれているのかで観察していくと男子短距離：10 男子長距離：9 女子短距離：9 女子長距離：9 とわかります。よってすべて確かに12未満です。

2：考える対象は男子長距離グループですが、グラフは文中にあるからとヒストグラムと考えるのは早計です。使うグラフの判断は、知りたいこととグラフの特性の組み合わせで考えます。知りたいのは、度数最大の階級に中央値が入っているかということです。ということは、度数最大の階級と中央値がわかるグラフを使うべきです。まず度数といえばヒストグラムです。度数の分布を示したものなので、度数が最大の階級値はヒストグラムから読み取るのが最適で、一番高い柱の170〜175のところであることがすぐわかります。他方、中央値はヒストグラムで見つけるのは困難で、箱ひげ図であれば一瞬です。四分位範囲の箱の中に引かれた縦線があるところが中央値で、176です。以上をあわせて考えると、170〜175の範囲に176は存在していないので、この選択肢は不成立であることがわかります。