【問題解説】センター試験平成30年度本試験 IA　第1問(4) - 数学が好きなサラリーマンのブログ

とてもひさびさのセンター更新。センター解説に何ヶ月使う気だと言われてしまいそうです。ゴメンナサイ。

で、さっそく問題へ。

f:id:mathbanker:20180315213336j:plain

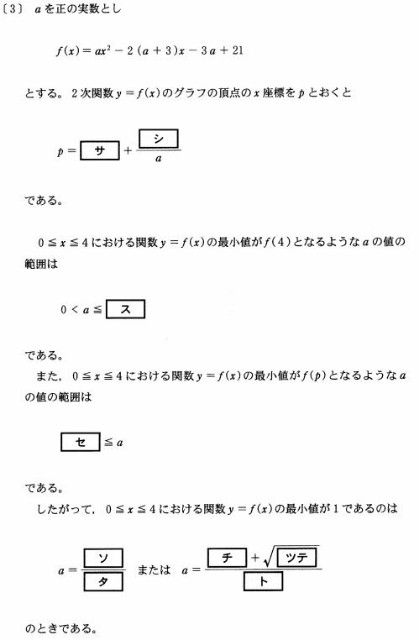
まず二次関数の頂点が問われているので、平方完成して頂点と馴染みのよい形にします。

$ f(x)=ax^{2}-2(a+3)x-3a+21 $

$ =a \left\{ x- \left(1+\dfrac{ 3 }{ a } \right) \right\}^{2}-\dfrac{9}{a}-4a+15 $

よって

$ p=1+\dfrac{3}{a} $

とわかります。ここで新しい文字$p$が出てきたので、その変域を確認しておきます。文字を置き換えたり、定義されたりして新しい文字がでてきたとき、その文字の中身にばかり目がいきがちですが、どんな範囲で成り立っている文字なのかという確認をすることが重要です。数学において、使われている文字がどんな集合に属しているのかということと、どんな形で定義されているのかということはセットです。

$a>0$なので、

$\dfrac{3}{a}>0$

$\therefore \ p=\dfrac{3}{a}+1>1$

となります。

さて、$0\leqq x \leqq 4$において$f(4)$が最小値になることから考えます。最小値は読んで字の如く、最も小さな値ということです。範囲の制限がなければ、二次関数の最小値は下に凸ならば頂点だし、上に凸ならば存在しません（頂点は最大値）。そして、二次関数の対称性から頂点に近いほど小さい値となっているか（下に凸）、大きくなっています（上に凸）。

そんなことわかってるよと思ってるかもしれませんが、こういうのをただの知識として持ってる人も少なくないと思います。持ってるだけの知識が自発作用的に役立つことって少ないです。持ってる知識は使う・武器にするという姿勢を忘れちゃいけません。

で、まず上に凸か下に凸かみてみると、最高次の係数が$a(>0)$だから下に凸です。$p>1$なので、頂点は$0\leqq x \leqq 4$の中にあってもいいし（つまり$0\leqq p \leqq 4$）、外にでていることもありえます（つまり$p>4$）。

で、いま最小値が$f(4)$です。これってどこかというと、$0\leqq x \leqq 4$の大きい方の端です。ここに固定されてます。$0\leqq p \leqq 4$だと、頂点$= f(4)$となってない限り、頂点が最小値であって、$f(4)$が最小値になってくれません。

ゆえに$p \geqq 4$のときを考えます。頂点が考えている範囲より大きい場所に位置しているので、$0\leqq x \leqq 4$の範囲内でみると$x$が大きいほど値は小さくなります。

$4 \leqq p=1+\dfrac{3}{a}$

$\Leftrightarrow \dfrac{1}{a} \geqq 1$

$\therefore a \leqq 1$

つぎに$f(p)$が最小値となる場合を考えます。つまり頂点が最小値になるときです。$0\leqq p \leqq 4$となっていればいいのですが、正確には先ほど求めた$p>1$を考慮して$1 <p \leqq 4$となります。

$1< p=\dfrac{3}{a}+1 \leqq 4$

$\Leftrightarrow 0<1\leqq a$

となります。

最後に最小値が1のときを考えます。問題文で「したがって」という言葉があります。この言葉は原因⇒「したがって」⇒結果という形を作ります。いま、この結果にあたるところを求めようとしているわけですが、その根拠がこの言葉以前のところにあると問題文は教えてくれています。

この「したがって」以前のところに根拠をみつけて問題を解くことがいわゆる問題文の流れに乗るということです。戻って探してみると、この問題の「$0\leqq x \leqq 4$における最小値が$1$」という文章と似たものが2カ所ありました。

「$0\leqq x \leqq 4$における最小値が$f(4)$」

「$0\leqq x \leqq 4$における最小値が$f(p)$」

です。これらがそもそも何だったかと振り返ると、頂点の位置によって最小値を取るところが変わるという違いで分岐されたものでした。$f(4)$と$f(p)$どちらかが最小値で、2つを合わせると考えている二次関数$f(x)$の定義域全体をカバーしています。頂点は$1<p$という条件があり、$1<p \leqq 4$のときは最小値$f(p)$、$p \geqq 4$のときは最小値$f(4)$となることが求まっていて、これで$f(x)$の頂点の移動範囲すべてをカバーできていることからわかります（このことがわかっていれば、スがわかればセは明らかなのでありました）。

で今回最小値が$1$となっているわけです。二次関数$f(x)$がこの$1$を与えるときの頂点がどこにあるのかで、$f(p)$型なのか$f(4)$型なのかが分かれます。それぞれ順番に検証してみればわかります。

まず$f(p)$型から考えると、$1$は頂点の$y$座標の値だったということになります。

$-\dfrac{9}{a}-4a+15=1$

となるようなaを求めればいいわけです。

$\Leftrightarrow 4a^{2} -14a+9=0$

$\therefore a=\dfrac{7 \pm \sqrt{13}}{4}$

$f(p)$型は$a \geqq 1$でした。$a=\dfrac{7 - \sqrt{13}}{4} <1$ なので、$f(p)$型のとき最小値が1になるような$a$は

$a=\dfrac{7 + \sqrt{13}}{4} $

とわかります。

$f(4)$型で最小値が1になるときは、$4$を代入したら$1$になればいいので

$f(4)=16a-8(a+3)-3a+21=1$

$\Leftrightarrow a=\dfrac{4}{5}$