【問題解説】センター試験平成29年度本試験 IA　第1問(続)

今回は前回の続きを解いていきます。

f:id:mathbanker:20170908101524j:plain

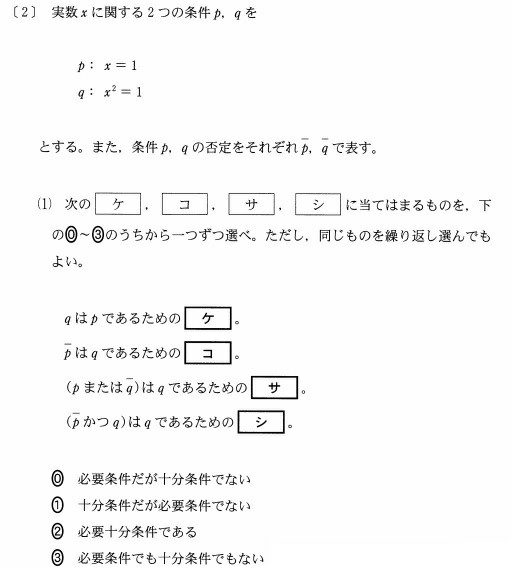
必要条件・十分条件の問題です。では、まずは定義から。

命題$P$、$Q$に対して $P\Rightarrow Q$が真であるとき
$P$を$Q$である為の十分条件
$Q$を$P$である為の必要条件
といい、必要条件かつ十分条件であるとき必要十分条件という。

普段の会話でも時々耳にする言葉です。でもそこを掘り下げるとコラムチックになるのでここでは割愛。

必要条件・十分条件を考えるとき、僕が高校時代なんかは問題文の日本語に矢印ひかせて、成立する向きをもって判断するなんてことがありましたが、日本語の書き方次第なところがあるので、このやり方は今にして振り返ると少しリスクを伴います。

定義にもある通り、まずもって
命題に対して $P\Rightarrow Q$が真である
が大前提で、この$P$、$Q$に与えられた名前がそれぞれ十分条件、必要条件なわけです。「・・・である為の」という日本語が入っているから複雑に思える人がいるのかもしれませんが、$P$が十分条件で$Q$が必要条件です。 前提となる「○○ならば△△」という文が成り立つことがすべてで、この文が作れればあとは名前を呼ぶだけです。

ちなみにこの文を作るために役に立つのが、図の利用です。十分条件と必要条件は図で表すと、 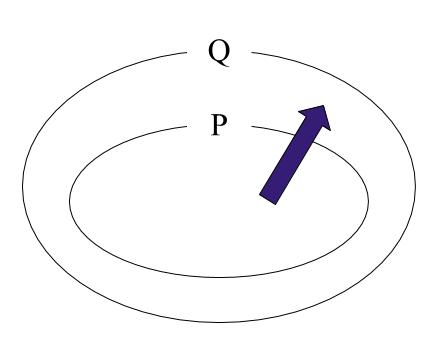f:id:mathbanker:20170911004657j:plain こんな感じです。ご参考。

今回の問題においては、
$p：x=1$
$q：x^{2}=1$
となっています。この２つの命題に対し、成り立つのは $$ p \Rightarrow q $$ です。$q$は表現を変えると$q：x=1,-1$なので(カンマは『または』)、上の図のこの問題バージョンを考えると 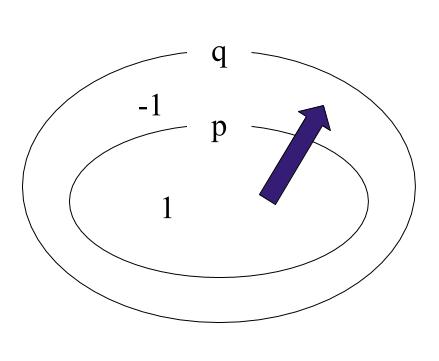f:id:mathbanker:20170911004252j:plain となります。

「$p$ ならば $q$ 」という文が成り立つことがわかったので、あとは名前を呼ぶだけです。
$p$ は必要条件で、$q$が十分条件です（ケ）。

こんな感じで機械的に考えていけば簡単です。
次は$\overline{p}$と$q$です。 具体的にすると、${x\neq 1}$と${x^{2}=1}$です。これは
$ p \Rightarrow q$
$q \Rightarrow p $
どちらも成り立ちません。${x\neq 1}$は$1$以外の実数全体が当てはまります。なので 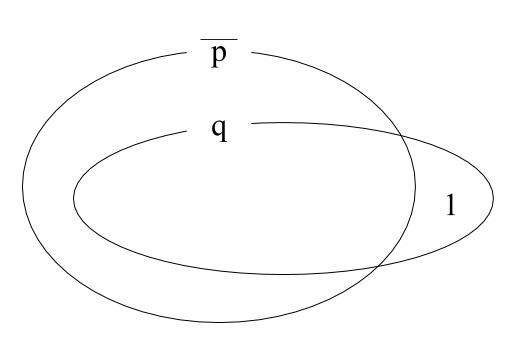f:id:mathbanker:20170911010355j:plain こういう図になります。しっかり包含関係が成り立たないと必要も十分も言えません。

どんどんいきましょう。（$p$または$\overline{q}$）と$q$です。
$p$または$\overline{q}$ の正体がわかりにくいので、具体化します。 $p$は$x=1$で、$\overline{q}$は$x$が$1$と$-1$ 以外ならOKということです。『または』とあるのでどちらかを満たしていればよく、$-1$以外の実数ならば当てはまります。つまり
$p$または$\overline{q}$：${x\neq -1}$
$q：x^{2}=1$
です。これは、前問が${x\neq 1}$と${x^{2}=1}$だったで、${x\neq 1}$が${x\neq -1}$になっただけです。ゆえに同じ議論でこれも必要条件でも十分条件でもありません。

最後に、（$\overline{p}$かつ$q$）と$q$です。これも（$\overline{p}$かつ$q$）を具体化して考えます。 $\overline{p}$かつ$q$は、${x\neq 1}$と${x=1,-1}$を同時に満たすような$x$です。それは${x=-1}$しかありません。ゆえに $\overline{p}$かつ$q$：$x=-1$
$q$：$x=1,-1$
は、$(\overline{p}$かつ$q) \Rightarrow q$の向きだけが成立します。ゆえに$(\overline{p}$かつ$q)は十分条件で、必要条件ではありません（シ）。

日本語の「必要」と「十分」にある語感から判断するのではなく、「○○ならば△△」が成り立つ文を考えて、名前を呼ぶだけでいいんです。 図で考えると整理しやすいことが多いですが、それはつまり集合で考えるということです。どういう集合関係があるのか、包含関係があるのかを探せば解けます。集合で一方が一方に属しているのかどうかから「○○ならば△△」という作文を行うプロセスを徹底し、無駄に日本語感覚に挑戦しないことです。

で、最後に宣伝。よろしく。